题目内容
函数y=lg（2sinx-
）的定义域为 ．
| 3 |
考点：正弦函数的单调性
专题：三角函数的图像与性质
分析：依题意，解不等式2kπ+
＜x＜2kπ+
（k∈Z）即可求得函数y=lg（2sinx-
）的定义域．
| π |
| 3 |
| 2π |
| 3 |
| 3 |
解答：
解：由2sinx-
＞0得：sinx＞
，
所以，2kπ+
＜x＜2kπ+
，k∈Z．
所以函数y=lg（2sinx-
）的定义域为（2kπ+
，2kπ+
），k∈Z．
故答案为：（2kπ+
，2kπ+
），k∈Z．
| 3 |
| ||
| 2 |
所以，2kπ+
| π |
| 3 |
| 2π |
| 3 |
所以函数y=lg（2sinx-
| 3 |
| π |
| 3 |
| 2π |
| 3 |
故答案为：（2kπ+
| π |
| 3 |
| 2π |
| 3 |
点评：本题考查对数函数的定义域，着重考查正弦函数的单调性，考查解不等式的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，棱长为2的正方体ABCD-A1B1C1D1中，E为棱C1D1上的动点，F为棱BC的中点．
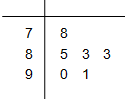为了了解某同学的数学学习情况，对他的6次数学测试成绩（满分100分）进行统计，作出的茎叶图如图所示，则下列关于该同学数学成绩的说法正确的是（ ）| A、中位数为83 |
| B、平均数为85 |
| C、众数为85 |
| D、方差为19 |
下列判断正确的是（ ）
| A、命题“a，b都是偶数，则a+b是偶数”的逆否命题是“若a+b不是偶数，则a，b 都不是偶数 |
| B、若“p或q”为假命题，则“￢p且￢q”是假命题 |
| C、已知a，b，c是实数，关于x的不等式ax2+bx+c≤0的解集是空集，必有a＞0且∨≤0 |
| D、x2≠y2?x≠y且x≠-y |
班级需要在甲、乙、丙三位同学中随机的抽取两位参加一项活动，则正好抽到的是甲乙的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|