题目内容
15.函数f(x)=$\frac{lnx+2}{x}$+a(x-1)-2.(1)当a=0时,求函数f(x)的极值;
(2)若对任意x∈(0,1)∪(1,+∞),不等式$\frac{f(x)}{1-x}$<$\frac{a}{x}$恒成立,求实数a的取值范围.
分析 (1)先求导,根据导数和函数的极值的关系即可求出,
(2)原不等式等价于$\frac{f(x)}{x-1}$+$\frac{a}{x}$>0,即$\frac{xf(x)+a(x-1)}{x-1}$>0,构造函数g(x)=lnx+a(x2-1)-2(x-1),根据导数和函数的最值得关系,分类讨论即可证明
解答 解:(1)当a=0时,f(x)=$\frac{lnx+2}{x}$-2.x>0,
∴f′(x)=$\frac{-1-lnx}{{x}^{2}}$
令f′(x)=0,解得x=$\frac{1}{e}$,
当f′(x)>0时,即0<x<$\frac{1}{e}$,函数单调递增,
当f′(x)<0时,即x>$\frac{1}{e}$,函数单调递减,
∴当x=$\frac{1}{e}$时,函数f(x)有极大值,极大值为f($\frac{1}{e}$)=e-2,无极小值;
(2)原不等式等价于$\frac{f(x)}{x-1}$+$\frac{a}{x}$>0,即$\frac{xf(x)+a(x-1)}{x-1}$>0,
∴$\frac{1}{x-1}$[lnx+a(x2-1)-2(x-1)]>0,
令g(x)=lnx+a(x2-1)-2(x-1),g(1)=0,
∴g′(x)=$\frac{1}{x}$+2ax-2=$\frac{2a{x}^{2}-2x+1}{x}$,
∵$\frac{1}{x-1}$[lnx+a(x2-1)-2(x-1)]>0,
g(2)=ln2+3a-2>0⇒a>$\frac{2-ln2}{3}$>0,
①当a≥$\frac{1}{2}$时,2ax2-2x+1≥x2-2x+1≥(x-1)2>0,
∴g′(x)>0,
∴g(x)在(0,+∞)上单调递增,
∴x∈(0,1),g(x)<0,x∈(1,+∞),g(x)>0,
∴$\frac{1}{x-1}$g(x)>0,
②当0<a<$\frac{1}{2}$时,令2ax2-2x+1=0,解得x=$\frac{1+\sqrt{1-a}}{2a}$>1,
∴x∈(1,$\frac{1+\sqrt{1-a}}{2a}$)时,g′(x)<0,函数g(x)单调递减,
∴g(x)<g(1)=0,
∴$\frac{1}{x-1}$g(x)<0,不合题意,舍去,
综上所述a≥$\frac{1}{2}$
点评 本题考查了函数的单调性,极值,零点的基础知识,考查学生运算求解与推理论证的能力,运用导数工具解决函数与方程,不等式综合问题的能力,考查了数形结合,分类与整合,转化与化归的数学思想,属于难题

| A. | 1:1:3 | B. | 1:2:3 | C. | 1:3:2 | D. | 1:4:1 |
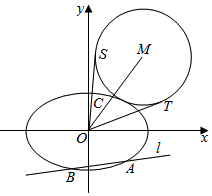 在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.
在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.