题目内容
5.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{5}}{3}$,右顶点A(3,0),直线l与x轴交于点A,与y轴交于点E.(1)求椭圆C的方程;
(2)若直线l与椭圆C的另一交点为D,P为弦AD的中点,是否存在着定点Q,使得OP⊥EQ恒成立?若存在,求出Q点的坐标,若不存在,请说明理由;
(3)若OM∥l,交椭圆C于点M,在(2)的条件下,求$\frac{|AD|+|AE|}{|OM|}$的最小值.
分析 (1)由题意可知:a=3,e=$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$,c=$\sqrt{5}$,则b2=a2-c2=4,即可求得椭圆方程;
(2)设直线l的方程,代入椭圆方程,利用中点坐标公式,求得D坐标,根据中点坐标公式,即可求得P点坐标,分别求得OP及EQ的斜率,由kOP•kEQ=-1,即可求得4n+(12-9m)k=0,即可求得m和n值,求得Q点坐标;
(3)设直线OM的方程y=kx,代入椭圆方程,求得xM,$\frac{|AD|+|AE|}{|OM|}$=$\frac{丨{x}_{D}-3丨+丨{x}_{E}-3丨}{丨{x}_{M}丨}$=$\frac{1}{2}$($\frac{9{k}^{2}+12}{\sqrt{9{k}^{2}+4}}$)=$\frac{1}{2}$($\sqrt{9{k}^{2}+4}$+$\frac{8}{\sqrt{9{k}^{2}+4}}$),根据基本不等式的性质,即可求得答案.
解答 解:(1)由椭圆右顶点A(3,0),a=3,椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$,则c=$\sqrt{5}$,
b2=a2-c2=4,
∴椭圆的标准方程:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$;
(2)由题意可知,直线l的斜率存在且不为0,设直线l的方程y=k(x-3),
$\left\{\begin{array}{l}{y=k(x-3)}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,消去y,整理得:(9k2+4)x2-54k2x+81k2-36=0,
设D(xD,yD),则3xD=$\frac{81{k}^{2}-36}{9{k}^{2}+4}$,则xD=$\frac{27{k}^{2}-12}{9{k}^{2}+4}$,yD=k(xD-3)=-$\frac{24k}{9{k}^{2}+4}$,
∴D($\frac{27{k}^{2}-12}{9{k}^{2}+4}$,-$\frac{24k}{9{k}^{2}+4}$),由P为弦AD的中点,则P($\frac{27{k}^{2}}{9{k}^{2}+4}$,-$\frac{12k}{9{k}^{2}+4}$),
∴直线OP的斜率kOP=-$\frac{4}{9k}$,
对于直线l的方程y=k(x-3),令x=0,则E(0,-3k),
假设存在定点Q(m,n),m≠0,满足OP⊥EQ,
直线EQ的斜率kEQ=$\frac{n+3k}{m}$,
∴kOP•kEQ=-$\frac{4}{9k}$•$\frac{n+3k}{m}$=-1,整理得4n+12k-9km=0,
由4n+(12-9m)k=0恒成立,则$\left\{\begin{array}{l}{12-9m=0}\\{4n=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=\frac{4}{3}}\\{n=0}\end{array}\right.$,
则定点Q的坐标为($\frac{4}{3}$,0);
(3)由OM∥l,则直线OM的方程y=kx,设M(xM,yM),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1}\\{y=kx}\end{array}\right.$,解的:xM=±$\frac{6}{\sqrt{9{k}^{2}+4}}$,
由$\frac{|AD|+|AE|}{|OM|}$=$\frac{丨{x}_{D}-3丨+丨{x}_{E}-3丨}{丨{x}_{M}丨}$=$\frac{6-\frac{27{k}^{2}-12}{9{k}^{2}+4}}{\frac{6}{\sqrt{9{k}^{2}+4}}}$=$\frac{1}{2}$($\frac{9{k}^{2}+12}{\sqrt{9{k}^{2}+4}}$)=$\frac{1}{2}$($\sqrt{9{k}^{2}+4}$+$\frac{8}{\sqrt{9{k}^{2}+4}}$)≥2$\sqrt{\sqrt{9{k}^{2}+4}×\frac{8}{\sqrt{9{k}^{2}+4}}}$=$\frac{1}{2}$×2×2$\sqrt{2}$=2$\sqrt{2}$,
当且仅当$\sqrt{9{k}^{2}+4}$=$\frac{8}{\sqrt{9{k}^{2}+4}}$,即k=±$\frac{2}{3}$时,取等号,
∴当k=±$\frac{2}{3}$时,$\frac{|AD|+|AE|}{|OM|}$的最小值2$\sqrt{2}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查中点坐标公式,直线的斜率公式,考查基本不等式的性质,考查计算能力,属于中档题.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | b<c<a |
 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
 如图 已知四边形 ABCD 为直角梯形,AB⊥AD,DC∥AB,且边 AB、AD、DC 的长分别为 7cm,4cm,4cm,分别以 AB、AD、DC 三边所在直线为旋转轴,求所得几何体体积.
如图 已知四边形 ABCD 为直角梯形,AB⊥AD,DC∥AB,且边 AB、AD、DC 的长分别为 7cm,4cm,4cm,分别以 AB、AD、DC 三边所在直线为旋转轴,求所得几何体体积.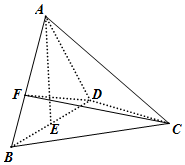 如图,在三棱锥A-BCD中,已知△ABD,△BCD都是边长为2的等边三角形,E为BD中点,且AE⊥平面BCD,F为线段AB上一动点,记$\frac{BF}{BA}=λ$.
如图,在三棱锥A-BCD中,已知△ABD,△BCD都是边长为2的等边三角形,E为BD中点,且AE⊥平面BCD,F为线段AB上一动点,记$\frac{BF}{BA}=λ$.