题目内容
函数y=log2
的值域为( )
| 2 |
| x2+1 |
| A、[1,+∞) |
| B、(0,1] |
| C、(-∞,1] |
| D、(-∞,1) |
考点:函数的值域
专题:函数的性质及应用
分析:设t=
,函数y=log2
,则转化为y=log
,0<t≤2,求解.
| 2 |
| x2+1 |
| 2 |
| x2+1 |
t 2 |
解答:
解:设t=
,函数y=log2
,
则y=log
,0<t≤2,
根据对数函数的单调性可知:log
≤1,
故选:C
| 2 |
| x2+1 |
| 2 |
| x2+1 |
则y=log
t 2 |
根据对数函数的单调性可知:log
t 2 |
故选:C
点评:本题考查了对数函数的单调性,运用换元的方法转化求解.

练习册系列答案
相关题目
下列函数中为偶函数,且在区间(0,+∞)上为增函数的是( )
| A、y=3-x | ||
| B、y=|x| | ||
C、
| ||
| D、y=-x2+4 |
设等差数列{an}满足:a1+a4+a7=12,则a1+a2+a3+…+a7=( )
| A、14 | B、21 | C、28 | D、35 |
设集合A={-1,2,3},B={2a+4,a2+1},A∩B={2},则满足条件的实数a( )
| A、只有一个 | B、有两个 |
| C、有3个 | D、不存在 |
已知集M={x|y=
},N={x|x=t2,t∈M},则集合M∩N等于( )
| 1-x2 |
| A、M | B、N | C、R | D、ϕ |
已知函数f(x)=
,则f(-7)=( )
|
| A、1 | B、4 | C、16 | D、49 |
将函数y=
cosx+sinx(x∈R)的图象向左平移m(m>0)个长度单位后,所得到的图象关于原点对称,则m的最小值是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
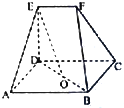 已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=
已知矩形ABCD,ED⊥平面ABCD,EF∥DC,EF=DE=AD=