题目内容
F是椭圆C:
+
=1的右焦点,定点A(-1,1),M是椭圆上的动点,则
|MA|+|MF|的最小值为 .
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:利用圆锥曲线的统一定义
=e=
,结合题意化简得|AM|+2|MF|=|AM|+|MN|,根据平面几何性质得当A、M、N共线于垂直于右准线的一条直线上时,|AM|+2|MF|取得最小值,由此即可算出答案.
| |MF| |
| |MN| |
| 1 |
| 2 |
解答:
 解:根据椭圆方程得e=
解:根据椭圆方程得e=
=
∴
|MA|+|MF|=
(|MA|+2|MF|),
根据椭圆的第二定义:
过A作右准线的垂线,交于N点,
右准线方程为x=4.
则|MA|+2|MF|=|MA|+|MN|≥|AN|
∵|AN|=4+1=5.
故答案为:
.
 解:根据椭圆方程得e=
解:根据椭圆方程得e=| c |
| a |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
根据椭圆的第二定义:
过A作右准线的垂线,交于N点,
右准线方程为x=4.
则|MA|+2|MF|=|MA|+|MN|≥|AN|
∵|AN|=4+1=5.
故答案为:
| 5 |
| 2 |
点评:本题考查了椭圆的第二定义,以及三点共线时和最小的思想,体现了数形结合思想.

练习册系列答案
相关题目
sin(-
π)的值等于( )
| 14 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
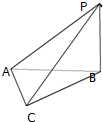 如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.
如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.