题目内容
1.已知向量$\overrightarrow{a}$=(sinθ,1),$\overrightarrow{b}$=(cosθ,$\frac{1}{2}$),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则2cos($\frac{3π}{2}$+2θ)+$\frac{1}{2}$cos2θ的值为( )| A. | $\frac{13}{10}$ | B. | $\frac{19}{10}$ | C. | $\frac{3}{2}$ | D. | -2 |
分析 根据$\overrightarrow{a}$∥$\overrightarrow{b}$,可得$\frac{1}{2}$sinθ=cosθ,从而tanθ=2.利用“弦化切”思想,根据诱导公式和二倍角化简可得答案.
解答 解:由题意,向量$\overrightarrow{a}$=(sinθ,1),$\overrightarrow{b}$=(cosθ,$\frac{1}{2}$),
∵$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴$\frac{1}{2}$sinθ=cosθ,
从而tanθ=2.
那么:2cos($\frac{3π}{2}$+2θ)+$\frac{1}{2}$cos2θ=2sin2θ+$\frac{1}{2}$cos2θ=4sinθcosθ+$\frac{1}{2}$cos2θ$-\frac{1}{2}$sin2θ=$\frac{4sinθcosθ+\frac{1}{2}co{s}^{2}θ-\frac{1}{2}si{n}^{2}θ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{4tanθ+\frac{1}{2}-\frac{1}{2}×ta{n}^{2}θ}{1+ta{n}^{2}θ}$=$\frac{13}{10}$.
故选A
点评 本题考查了诱导公式和二倍角化简计算能力和同角三角函数关系式的计算.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知集合A={x|1<x<3},B={x|y=log2(2-x)},则A∩B=( )
| A. | (0,3) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
13.已知全集U={0,1,2,3,4,5},集合A={0,2,4},B={1,3,4},则(∁UA)∩B=( )
| A. | {4} | B. | {1,3} | C. | {1,3,4,5} | D. | {0,1,2,3,4} |
10.设集合A={-1,0,1},B={x|x2-2x-3≤0},则A∩B=( )
| A. | {-1,0,1} | B. | {0} | C. | (-1,1) | D. | (-1,3) |
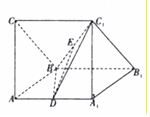 在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点.