题目内容
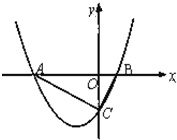 如图,已知抛物线y=
如图,已知抛物线y=| 1 |
| 2 |
(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)利用一元二次方程的根与系数的关系即可得出;
(2)利用△CEF的面积是△BEF面积的2倍,可得CF=2FB.再根据EF∥AC,可得
=
=
.即可得出.
(3)由抛物线的方程y=
x2+
x-2.令x=0,C(0,-2).可得直线AC的方程为:
+
=1.
设直线PQ的方程为:x=t(-4≤t≤0),由于PQ∥y轴.可得|PQ|=yQ-yP.再利用二次函数的单调性即可得出.
(2)利用△CEF的面积是△BEF面积的2倍,可得CF=2FB.再根据EF∥AC,可得
| AE |
| EB |
| CF |
| FB |
| 2 |
| 1 |
(3)由抛物线的方程y=
| 1 |
| 2 |
| 3 |
| 2 |
| x |
| -4 |
| y |
| -2 |
设直线PQ的方程为:x=t(-4≤t≤0),由于PQ∥y轴.可得|PQ|=yQ-yP.再利用二次函数的单调性即可得出.
解答:
解:(1)∵抛物线与x轴交于A(-4,0)和B(1,0),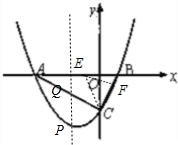
∴
,解得b=
,c=-2.
∴抛物线的方程为y=
x2+
x-2.
(2)如图所示,
∵△CEF的面积是△BEF面积的2倍,
∴CF=2FB,
∵EF∥AC,
∴
=
=
.
∵A(-4,0),B(1,0).
∴xE-(-4)=2(1-xE),解得xE=-
.
∴E(-
,0).
(3)由抛物线的方程为y=
x2+
x-2.
令x=0,得y=-2.即(0,-2).
∴直线AC的方程为:
+
=1,化为x+2y+4=0.
设直线PQ的方程为:x=t(-4≤t≤0),
∵PQ∥y轴.
∴|PQ|=yQ-yP
=(-
t-2)-(
t2+
t-2)
=-
t2-2t
=-
(t+2)2+2,
当t=-2时,|PQ|取得最大值2.
此时yP=
×(-2)2+
×(-2)-2=-3,∴P(-2,-3).

∴
|
| 3 |
| 2 |
∴抛物线的方程为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)如图所示,
∵△CEF的面积是△BEF面积的2倍,
∴CF=2FB,
∵EF∥AC,
∴
| AE |
| EB |
| CF |
| FB |
| 2 |
| 1 |
∵A(-4,0),B(1,0).
∴xE-(-4)=2(1-xE),解得xE=-
| 2 |
| 3 |
∴E(-
| 2 |
| 3 |
(3)由抛物线的方程为y=
| 1 |
| 2 |
| 3 |
| 2 |
令x=0,得y=-2.即(0,-2).
∴直线AC的方程为:
| x |
| -4 |
| y |
| -2 |
设直线PQ的方程为:x=t(-4≤t≤0),
∵PQ∥y轴.
∴|PQ|=yQ-yP
=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 1 |
| 2 |
=-
| 1 |
| 2 |
当t=-2时,|PQ|取得最大值2.
此时yP=
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了考查了一元二次方程根与系数的关系、平行线分线段成比例定理、三角形的面积计算公式、二次函数的单调性、直线的方程等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
复数(
)2(i是虚数单位)化简的结果是( )
| 1-i |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
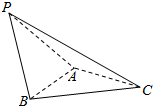 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.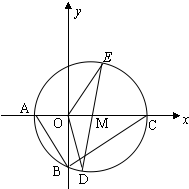 如图,△ABC中,
如图,△ABC中,