题目内容
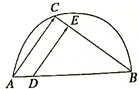如图，半圆的直径AB=6，C是半圆上的一点，D、E分别是AB、BC上的点，且AD=1，BE=4，DE=3．（1）求证：
| AC |
| DE |
（2）求|
| AC |
考点：向量的模,平行向量与共线向量
专题：平面向量及应用
分析：（1）由题意求出BD得DE2+BE2=BD2，即∠DEB=90°，由AB是圆的直径得∠ACB=90°，可证明结论；
（2）根据AC∥DE得
=
，把数据代入求出AC的值，就是|
|．
（2）根据AC∥DE得
| DE |
| AC |
| DB |
| AB |
| AC |
解答：
证明：（1）由题意得，AB=6，AD=1，则BD=5，
因为BE=4，DE=3，所以DE2+BE2=BD2，即∠DEB=90°，
因为AB是圆的直径，所以∠ACB=90°，
则AC∥DE，即
∥
；
解：（2）因为AC∥DE，所以
=
，
即AC=
=
=
，
所以|
|=
．
因为BE=4，DE=3，所以DE2+BE2=BD2，即∠DEB=90°，
因为AB是圆的直径，所以∠ACB=90°，
则AC∥DE，即
| AC |
| DE |
解：（2）因为AC∥DE，所以
| DE |
| AC |
| DB |
| AB |
即AC=
| DE•AB |
| DB |
| 3×6 |
| 5 |
| 18 |
| 5 |
所以|
| AC |
| 18 |
| 5 |
点评：本题考查平面几何知识在向量中的应用，属于基础题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若
•
=
•
=1，那么c等于（ ）
| AB |
| AC |
| BA |
| BC |
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
设集合M={a，a+1}，N={x∈R|x2≤4}，若M∪N=N，则实数a的取值范围为（ ）
| A、[-1，2] |
| B、[-2，1] |
| C、[-2，2] |
| D、（-∞，-2]∪[2，+∞） |