题目内容
在某次考试中，要从20道题中随机地抽出6道题，若考生至少能答对其中的4道题即可通过：若至少能答对其中的5道题就获得优秀，已知某考生能答对其中的10道题，并且知道他在这次考试中已经通过，则他获得优秀成绩的概率是 ．
考点：互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题：概率与统计
分析：由条件根据条件概率的求法，并注意互斥事件概率计算公式的合理运用，求得他获得优秀成绩的概率．
解答：
解：设“他能答对其中的6道题”为事件A，“他能答对其中的5道题”为事件B，“他能答对其中的4道题”为事件C，
设“他考试通过”为事件D，“他考试获得优秀”为事件E．
则由题意可得D=A∪B∪C，E=A∪B，且A、B、C两两互斥．
P（D）=P（A）+P（B）+P（C）=
=
．
又AD=A，BD=B，∴P（E|D）=P（A|D）+P（B|D）=
=
=
=
，
故答案为：
设“他考试通过”为事件D，“他考试获得优秀”为事件E．
则由题意可得D=A∪B∪C，E=A∪B，且A、B、C两两互斥．
P（D）=P（A）+P（B）+P（C）=
| ||||||||||
|
| 12180 | ||
|
又AD=A，BD=B，∴P（E|D）=P（A|D）+P（B|D）=
| P(AD)+P(BD) |
| P(D) |
| P(A)+P(B) |
| P(D) |
| ||||||||||||||
|
| 13 |
| 58 |
故答案为：
| 13 |
| 58 |
点评：本题考查条件概率的求法，解题时要认真审题，注意互斥事件概率计算公式的合理运用，属于基础题．
练习册系列答案
相关题目
已知
，
是空间两个单位向量，且
•
＞0，设向量
=2
+
，
=-3
+2
，且＜
，
＞
，则＜
，
＞为（ ）
| m |
| n |
| m |
| n |
| a |
| m |
| n |
| b |
| m |
| n |
| a |
| b |
| 2π |
| 3 |
| m |
| n |
| A、30° | B、40° |
| C、90° | D、120° |
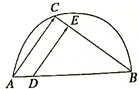如图，半圆的直径AB=6，C是半圆上的一点，D、E分别是AB、BC上的点，且AD=1，BE=4，DE=3．
如图，求f（a）并估计f′（a）．