题目内容
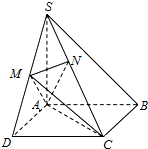 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.(Ⅰ)求证:SB∥平面ACM;
(Ⅱ)求证:直线SC⊥平面AMN;
(Ⅲ)求直线CM与平面AMN所成角的余弦值.
考点:直线与平面所成的角,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连结BD交AC于E,连结ME,由已知得ME∥SB,由此能证明SB∥平面ACM.
(Ⅱ)由条件有DC⊥SA,DC⊥DA,从而AM⊥DC,又AM⊥SD.从而AM⊥平面SDC,由此能证明SC⊥平面AMN.
(Ⅲ)由已知推导出∠CMN为所求的直线CM与面AMN所成的角,由此能求出直线CM与平面AMN所成角的余弦值.
(Ⅱ)由条件有DC⊥SA,DC⊥DA,从而AM⊥DC,又AM⊥SD.从而AM⊥平面SDC,由此能证明SC⊥平面AMN.
(Ⅲ)由已知推导出∠CMN为所求的直线CM与面AMN所成的角,由此能求出直线CM与平面AMN所成角的余弦值.
解答:
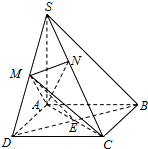 (Ⅰ)证明:连结BD交AC于E,连结ME.
(Ⅰ)证明:连结BD交AC于E,连结ME.
∵ABCD是正方形,∴E是BD的中点.
∵M是SD的中点,∴ME是△DSB的中位线.
∴ME∥SB.
又∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM.
(Ⅱ)证明:由条件有DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,∴AM⊥DC.
又∵SA=AD,M是SD的中点,∴AM⊥SD.
∴AM⊥平面SDC.∴SC⊥AM.
由已知SC⊥AN,∴SC⊥平面AMN.
(Ⅲ)解:由(Ⅱ)知CN⊥面AMN,则直线CM在面AMN内的射影为NM,
∴∠CMN为所求的直线CM与面AMN所成的角.
又SA=AB=2,∴在Rt△CDM中CD=2,MD=
∴CM=
又SC=
=2
由△SNM∽△SDC可得
=
∴MN=
.∴cos∠CMN=
=
∴直线CM与平面AMN所成角的余弦值为
 (Ⅰ)证明:连结BD交AC于E,连结ME.
(Ⅰ)证明:连结BD交AC于E,连结ME.∵ABCD是正方形,∴E是BD的中点.
∵M是SD的中点,∴ME是△DSB的中位线.
∴ME∥SB.
又∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM.
(Ⅱ)证明:由条件有DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,∴AM⊥DC.
又∵SA=AD,M是SD的中点,∴AM⊥SD.
∴AM⊥平面SDC.∴SC⊥AM.
由已知SC⊥AN,∴SC⊥平面AMN.
(Ⅲ)解:由(Ⅱ)知CN⊥面AMN,则直线CM在面AMN内的射影为NM,
∴∠CMN为所求的直线CM与面AMN所成的角.
又SA=AB=2,∴在Rt△CDM中CD=2,MD=
| 2 |
| 6 |
又SC=
| SA2+AC2 |
| 3 |
由△SNM∽△SDC可得
| MN |
| CD |
| SM |
| SC |
| ||
| 3 |
| MN |
| CM |
| 1 |
| 3 |
∴直线CM与平面AMN所成角的余弦值为
| 1 |
| 3 |
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,考查直线与平面所成角的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
如图所示程序框图,若输入N=3,则输出的S=( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={1,2,3,4},B={3,4,5,6,7},则A∪B等于( )
| A、{1,2,3,4,3,4,5,6,7} |
| B、{3,4} |
| C、{1,2,3,4,5,6,7} |
| D、∅ |
若向量
=(-1,0,1),向量
=(2,0,k),且满足向量
∥
,则k等于( )
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
 如图已知四棱锥P-ABCD中,底面ABCD是菱形,AB=PA=PD=2,∠ABD=60°,E是AD的中点,点Q是PC的中点.
如图已知四棱锥P-ABCD中,底面ABCD是菱形,AB=PA=PD=2,∠ABD=60°,E是AD的中点,点Q是PC的中点.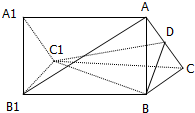 如图,已知A1B1C1-ABC是正三棱柱(底面为正三角形,且侧棱垂直底面),D是AC的中点.求证:AB1∥平面DBC1.
如图,已知A1B1C1-ABC是正三棱柱(底面为正三角形,且侧棱垂直底面),D是AC的中点.求证:AB1∥平面DBC1.