题目内容
函数f(x)=|lnx|-ax在区间(0,3]上有三个零点,则实数a的取值范围是 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:首先,画出函数y=|lnx|的图象,然后,借助于图象,结合在区间(0,3]上有三个零点,进行判断.
解答:
解:函数y=|lnx|的图象如图示:
当a≤0时,显然,不合乎题意,
当a>0时,如图示,
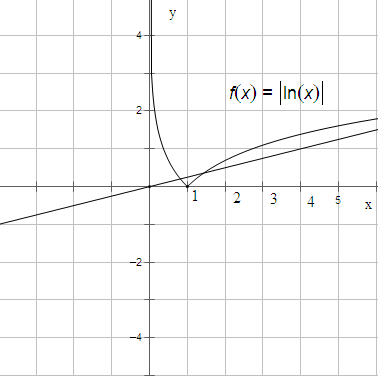
当x∈(0,1]时,存在一个零点,
当x>1时,f(x)=lnx,
可得g(x)=lnx-ax,(x∈(1,3])
g′(x)=
-a=,
若g′(x)<0,可得x>
,g(x)为减函数,
若g′(x)>0,可得x<
,g(x)为增函数,
此时f(x)必须在[1,3]上有两个交点,
∴
,
解得,
≤a<
,
在区间(0,3]上有三个零点时,
实数a的取值范围是[
,
),
故答案为:[
,
)
当a≤0时,显然,不合乎题意,
当a>0时,如图示,
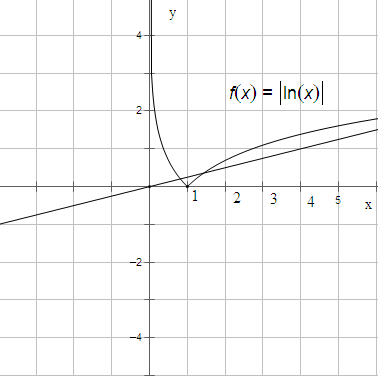
当x∈(0,1]时,存在一个零点,
当x>1时,f(x)=lnx,
可得g(x)=lnx-ax,(x∈(1,3])
g′(x)=
| 1 |
| x |
若g′(x)<0,可得x>
| 1 |
| a |
若g′(x)>0,可得x<
| 1 |
| a |
此时f(x)必须在[1,3]上有两个交点,
∴
|
解得,
| ln3 |
| 3 |
| 1 |
| e |
在区间(0,3]上有三个零点时,
实数a的取值范围是[
| ln3 |
| 3 |
| 1 |
| e |
故答案为:[
| ln3 |
| 3 |
| 1 |
| e |
点评:本题重点考查函数的零点,属于中档题,难度中等.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
在△ABC中,已知sinA+cosA=
,则角A为( )
| 1 |
| 5 |
| A、锐角 | B、直角 |
| C、钝角 | D、锐角或钝角 |
设α∈(0,
),β∈(
,π),若
=
,则下列结论一定正确的是( )
| π |
| 2 |
| π |
| 2 |
| 1-cosα |
| sinα |
| 1+cosβ |
| sinβ |
| A、sinα=sinβ |
| B、sinα=-cosβ |
| C、sinα=cosβ |
| D、sin2α=sin2β |