题目内容
投掷一枚正方体骰子(六个面上分别标有1,2,3,4,5,6),向上的面上的数字记为a,又n(A)表示集合的元素个数,A={x||x2+ax+3|=1,x∈R},则n(A)=4的概率为 .
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:由n(A)=4可得y=x2+ax+3 的最小值
<-1,a的取值是5或 6.再根据a的取值可能是6种,从而求得n(A)=4的概率.
| 12-a2 |
| 4 |
解答:
解:由n(A)=4知,函数y=|x2+ax+3|和y=1的图象有四个交点,
所以,y=x2+ax+3 的最小值
<-1,所以a的取值是5或6.
又因为a的取值可能是6种,故n(A)=4的概率是
=
,
故答案为:
.
所以,y=x2+ax+3 的最小值
| 12-a2 |
| 4 |
又因为a的取值可能是6种,故n(A)=4的概率是
| 2 |
| 6 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题主要考查函数的零点与方程的根的关系,古典概率及其计算公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知{an}是由正数组成的等比数列,Sn为其n项和.若a2a4=16,S3=7,则S4=( )
| A、15 | ||
| B、31 | ||
| C、63 | ||
D、
|
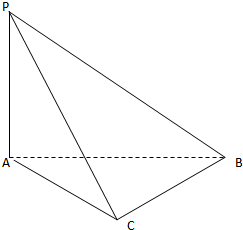 已知三棱锥P-ABC中,PA⊥AB,PA⊥AC,∠ACB=90°(如图)
已知三棱锥P-ABC中,PA⊥AB,PA⊥AC,∠ACB=90°(如图)
