题目内容
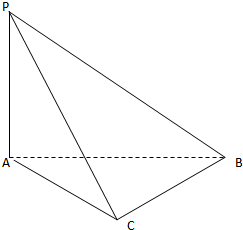 已知三棱锥P-ABC中,PA⊥AB,PA⊥AC,∠ACB=90°(如图)
已知三棱锥P-ABC中,PA⊥AB,PA⊥AC,∠ACB=90°(如图)(1)求证:PA⊥BC;
(2)若PA=AC=BC=1,求点C到平面PAB的距离.
考点:点、线、面间的距离计算,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)由已知条件推导出PA⊥平面ABC,由此能够证明PA⊥BC.
(2)由已知条件推导出平面PAB⊥平面ABC,过点C作CD⊥AB,交AB于点D,CD长就是点C到平面PAB的距离.由此能求出点C到平面PAB的距离.
(2)由已知条件推导出平面PAB⊥平面ABC,过点C作CD⊥AB,交AB于点D,CD长就是点C到平面PAB的距离.由此能求出点C到平面PAB的距离.
解答:
(1)证明:∵三棱锥P-ABC中,PA⊥AB,PA⊥AC,
AB∩AC=A, ∴PA⊥平面ABC,
∴PA⊥平面ABC,
∵BC?平面ABC,∴PA⊥BC.(2)∵PA⊥平面ABC,且PA?平面PAB,
∴平面PAB⊥平面ABC,
过点C作CD⊥AB,交AB于点D,
由直二面角的性质得CD⊥平面PAB,
∴CD长就是点C到平面PAB的距离.
在Rt△ABC中,∵AC=BC=1,∠ACB=90°,
∴AB=
,∴CD=
AB=
.
∴点C到平面PAB的距离为
.
AB∩AC=A,
 ∴PA⊥平面ABC,
∴PA⊥平面ABC,∵BC?平面ABC,∴PA⊥BC.(2)∵PA⊥平面ABC,且PA?平面PAB,
∴平面PAB⊥平面ABC,
过点C作CD⊥AB,交AB于点D,
由直二面角的性质得CD⊥平面PAB,
∴CD长就是点C到平面PAB的距离.
在Rt△ABC中,∵AC=BC=1,∠ACB=90°,
∴AB=
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴点C到平面PAB的距离为
| ||
| 2 |
点评:本题考查异面直线垂直的证明,考查点到直线的距离的求法,解题时要认真审题,注意合理地化空间问题为平面问题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 一个正三棱柱的每一条棱长都是a,则经过底面一边和相对侧棱的一个端点的截面(即图中△ACD)的面积为( )
一个正三棱柱的每一条棱长都是a,则经过底面一边和相对侧棱的一个端点的截面(即图中△ACD)的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E、F、G分别是各自所在棱的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E、F、G分别是各自所在棱的中点. 在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABBA1为矩形,AB=1,AA1=
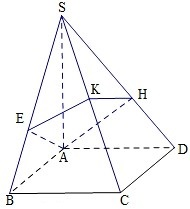 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.