题目内容
在等腰三角形△ABC中，底边BC=1，底角平分线BD交AC于点D，求BD的取值范围是 ．
考点：平行线分线段成比例定理
专题：选作题,立体几何
分析：利用角平分线的性质，结合BC-CD＜BD＜BC+BD，即可确定BD的取值范围．
解答：
解：因为底角B的角平分线BD交AC于点D
所以
=
设AB=AC=a，CD=x，则：
=
所以x=
因为BC-CD＜BD＜BC+BD
所以
＜BD＜
由题得：a＞0.5
所以
＜BD＜2
故答案为：（
，2）．
所以
| CD |
| BC |
| AD |
| AB |
设AB=AC=a，CD=x，则：
| a-x |
| a |
| x |
| 1 |
所以x=
| a |
| a+1 |
因为BC-CD＜BD＜BC+BD
所以
| 1 |
| a+1 |
| 2a+1 |
| a+1 |
由题得：a＞0.5
所以
| 2 |
| 3 |
故答案为：（
| 2 |
| 3 |
点评：本题考查角平分线的性质，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
为了调查某校学生体质健康达标情况，现采用随机抽样的方法从该校抽取了m名学生进行体育测试．根据体育测试得到了这m名学生各项平均成绩（满分100分），按照以下区间分为七组：[30，40），[40，50），[50，60），[60，70），[70，80），[80，90），[90，100），并得到频率分布直方图（如图），己知测试平均成绩在区间[30，60）有20人．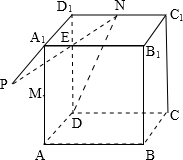
如图，在一封闭的正方体容器内装满水，M、N分别是AA1与C1D1的中点，由于某种原因，在D、M、N三点处各有一个小洞，为此容器内存水最多，问应将此容器如何放置？此时水的上表面的形状怎样？
如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）
A、（2+
| ||
| B、4π | ||
C、（2+2
| ||
| D、6π |