题目内容
已知函数f(x)=loga
是奇函数(a>0,a≠1).
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性;
(3)当a=
时,若对于[3,4]上的每一个x的值,不等式f(x)>(
)x+b恒成立,求实数b的取值范围.
| 1-mx |
| x-1 |
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性;
(3)当a=
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数恒成立问题,函数单调性的判断与证明,函数奇偶性的判断
专题:综合题,函数的性质及应用
分析:(1)利用奇函数的定义找关系求解出字母的值,注意对多解的取舍.
(2)利用y=
=1+
,可得在(1,+∞)内单调递减,即可得出结论.
(3)将恒成立问题转化为函数的最值问题,用到了分离变量的思想.
(2)利用y=
| x+1 |
| x-1 |
| 2 |
| x-1 |
(3)将恒成立问题转化为函数的最值问题,用到了分离变量的思想.
解答:
解:(1)∵f(x)是奇函数,∴f(-x)=-f(x).
∴
=
>0,
∴1-m2x2=1-x2,
∴m=±1.
检验m=1(舍),∴m=-1.
(2)由(1)知f(x)=loga
令y=
=1+
,则在(1,+∞)内单调递减
∴a>1时,f(x)在(1,+∞)内单调递增;0<a<1时,f(x)在(1,+∞)内单调递减.
(3)对[3,4]于上的每一个x的值,不等式f(x)>(
)x+b恒成立,即f(x)-(
)x>b恒成立.
令g(x)=f(x)-(
)x.只需g(x)min>b,
又易知g(x)=f(x)-(
)x在[3,4]上是增函数,
∴g(x)min=g(3)=-
.
∴b<-
时原式恒成立.
∴
| 1+mx |
| -x-1 |
| x-1 |
| 1-mx |
∴1-m2x2=1-x2,
∴m=±1.
检验m=1(舍),∴m=-1.
(2)由(1)知f(x)=loga
| x+1 |
| x-1 |
令y=
| x+1 |
| x-1 |
| 2 |
| x-1 |
∴a>1时,f(x)在(1,+∞)内单调递增;0<a<1时,f(x)在(1,+∞)内单调递减.
(3)对[3,4]于上的每一个x的值,不等式f(x)>(
| 1 |
| 2 |
| 1 |
| 2 |
令g(x)=f(x)-(
| 1 |
| 2 |
又易知g(x)=f(x)-(
| 1 |
| 2 |
∴g(x)min=g(3)=-
| 9 |
| 8 |
∴b<-
| 9 |
| 8 |
点评:本题是以对数函数为载体考查函数基本性质的小综合题,用到了函数奇偶性,函数单调性的定义.恒成立问题中求字母的取值范围问题往往通过分离变量转化为函数的最值问题,体现了等价转化的思想.

练习册系列答案
相关题目
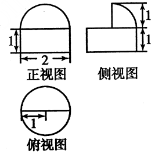
一个几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
某网站有10种资料,下载这些资料需要储值或点数,其中3种资料是精品资料,下载一个需扣5个储值,7种普通资料下载一个需扣4个点.某人现有20个点与10个储值,准备下载6种资料(每种资料至多下载一个,储值只用于下载精品资料,点只用于下载普通资料,点与储值够用即可,不必用完),则不同的下载方法的种数是( )
| A、62 | B、105 |
| C、168 | D、231. |
若双曲线C:
-
=1的一条渐近线的倾斜角为
,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、2或
| ||||
B、
| ||||
C、2或
| ||||
| D、2 |