题目内容
已知f(x)=
,当1≤x<3时,f(x)=(
)x,则f(2014)= .
| 1 |
| f(x+3) |
| 1 |
| 2 |
考点:函数的周期性,函数的值
专题:计算题,函数的性质及应用
分析:由题意可得f(x)=
=
=f(x+6),从而得到f(2014)=f(336×6-2)=f(-2)=
═
;从而解得.
| 1 |
| f(x+3) |
| 1 | ||
|
| 1 |
| f(-2+3) |
| 1 |
| f(1) |
解答:
解:∵f(x)=
=
=f(x+6),
故f(2014)=f(336×6-2)
=f(-2)=
=
=
=2;
故答案为:2.
| 1 |
| f(x+3) |
| 1 | ||
|
故f(2014)=f(336×6-2)
=f(-2)=
| 1 |
| f(-2+3) |
=
| 1 |
| f(1) |
| 1 | ||
|
故答案为:2.
点评:本题考查了函数的周期性的判断与应用,属于基础题.

练习册系列答案
相关题目
双曲线2x2-y2=1的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知平面α⊥平面β,交于直线l,且直线a?α,直线b?β,则下列命题错误的是( )
| A、若a∥b,则a∥l或b∥l |
| B、若a⊥b,则a⊥l且b⊥l |
| C、若直线a,b都不平行直线l,则直线a必不平行直线b |
| D、若直线a,b都不垂直直线l,则直线a必不垂直直线b |
 若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,则f(x)>f(2)的解集为( )
若程序框图如图所示,视x为自变量,y为函数值,可得函数y=f(x)的解析式,则f(x)>f(2)的解集为( )| A、(2,+∞) |
| B、(4,5] |
| C、(-∞,-2]4 |
| D、(-∞,-2)∪(3,5,5] |
 如图是某班第1和第2小组学生身高的茎叶图(单位:cm),则这两个小组学生身高中位数的等差中项为
如图是某班第1和第2小组学生身高的茎叶图(单位:cm),则这两个小组学生身高中位数的等差中项为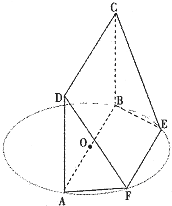 AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.