题目内容
已知集合A={x|m+1≤x≤2m},B={x|log2x≤3},当A∩B=∅时,实数m的取值范围是( )
| A、1<m<7 |
| B、m<1或m>7 |
| C、0≤m<7 |
| D、m≤0或m>7 |
考点:交集及其运算
专题:集合
分析:求出集合B,利用集合A∩B=∅时,建立条件关系即可得到结论.
解答:
解:B={x|log2x≤3}={x|0<x≤8},
若m+1>2m,即m<1,此时A=∅,满足条件,
当m≥1时,要使当A∩B=∅,
则m+1>8,解得m>7,
综上m<1或m>7,
故选:B
若m+1>2m,即m<1,此时A=∅,满足条件,
当m≥1时,要使当A∩B=∅,
则m+1>8,解得m>7,
综上m<1或m>7,
故选:B
点评:本题主要考查集合的关系的应用,要对A进行讨论.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
物体自由落体运动方程为s(t)=
gt2,若
=g=9.8m/s,那么下面说法正确的是( )
| 1 |
| 2 |
| lim |
| n→∞ |
| s(1+△t)-s(1) |
| △t |
| A、9.8m/s是0~1s这段时间内的平均速度 |
| B、9.8m/s是从1s到(1+△t)s这段时间内的速度 |
| C、9.8m/s是物体在t=1s这一时刻的速度 |
| D、9.8m/s是物体从1s到(1+△t)s这段时间内的平均速度 |
设a,b∈R,则“(a-b)3b2>0”是“a>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知f(x)=x3-3x,则函数h(x)=f[f(x)]-1的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
某汽车生产厂家准备推出10款不同的轿车参加车展,但主办方只能为该厂提供6个展位,每个展位摆放一辆车,并且甲、乙两款车不能摆放在1号展位,那么该厂家参展轿车的不同摆放方案有( )
A、C
| ||||
B、C
| ||||
C、C
| ||||
D、C
|
如果圆柱的轴截面周长为定值4,则圆柱体积的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
常说“便宜没好货”,这句话的意思是:“不便宜”是“好货”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
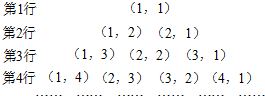 把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.
把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.