题目内容
 设函数f(x)=(1+x)α的定义域是[-1,+∞),其中常数α>0.
设函数f(x)=(1+x)α的定义域是[-1,+∞),其中常数α>0.(1)若α>1,求y=f(x)的过原点的切线方程.
(2)当α>2时,求最大实数A,使不等式f(x)>1+αx+Ax2对x>0恒成立.
(3)证明当α>1时,对任何n∈N*,有1<
| 1 |
| n |
| ||
| k=2 |
| k-1 |
| k |
| α |
| k |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求导数,分类讨论,利用导数的几何意义,可求y=f(x)的过原点的切线方程.
(2)令g(x)=f(x)-1-αx-Ax2,则g(0)=0,g′(x)=α(1+x)α-1-α-2Ax,显然g′(0)=0,且g′(x)的导函数为g″(x)=α(α-1)(1+x)α-2-2A.分类讨论,根据不等式f(x)>1+αx+Ax2对x>0恒成立,即可得出结论.
(3)证明对x∈(-1,0)恒有1<(1+x)α-αx<α,在此不等式中x=-
,-
,…,-
,不等式相加,即可证明结论.
(2)令g(x)=f(x)-1-αx-Ax2,则g(0)=0,g′(x)=α(1+x)α-1-α-2Ax,显然g′(0)=0,且g′(x)的导函数为g″(x)=α(α-1)(1+x)α-2-2A.分类讨论,根据不等式f(x)>1+αx+Ax2对x>0恒成立,即可得出结论.
(3)证明对x∈(-1,0)恒有1<(1+x)α-αx<α,在此不等式中x=-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
解答:
(1)解:∵f(x)=(1+x)α,∴f′(x)=α(1+x)α-1.
若切点为原点,由f′(0)=α知切线方程为y=αx+1;
若切点不为原点,设切点为(x0,(1+x0)α),
∴由切线过原点可知
=α(1+x0)α-1在(-1,+∞)内有唯一的根x0=
∵f′(
)=
,
∴切线方程为y=
x+(
)n
综上,所求切线有两条:y=αx+1和y=
x+(
)n;
(2)令g(x)=f(x)-1-αx-Ax2,则g(0)=0,g′(x)=α(1+x)α-1-α-2Ax,
显然g′(0)=0,且g′(x)的导函数为g″(x)=α(α-1)(1+x)α-2-2A.
若A≤
,则
≤1,由α>2知(1+x)α-2>1对x>0恒成立,从而对x>0恒有g″(x)>0,
即g′(x)在(0,+∞)上单调增,从而g′(x)>g′(0)=0对x>0恒成立,从而g(x)在(0,+∞)单调增,
∴g(x)>g(0)=0对x>0恒成立.
若A>
,则
>1,由α>2知知存在x0>0,使得(1+x)α-2<
对x∈(0,x0)恒成立,即g″(x)<0对x∈(0,x0)恒成立,
由g′(0)=0知存在x1>0,使得g′(x)<0对x∈(0,x1)恒成立,
∵g(0)=0,∴g(x)>0不能对x>0恒成立,
综上,最大实数A是
;
(3)证明:当α>1时,令h(x)=f(x)-αx,则h′(x)=α[(1+x)α-1-1],
∴x∈(-1,0)时,h′(x)<0,
即h(x)=f(x)-αx在[-1,0]上单调递减,∴h(0)<h(x)<h(-1)对x∈(-1,0)恒成立,
∵h(0)=1,h(-1)=α,
∴1<h(x)<α,
即对x∈(-1,0)恒有1<(1+x)α-αx<α,
在此不等式中x=-
,-
,…,-
∴1<(1-
)α+
<α,1<(1-
)α+
<α,1<(1-
)α+
<α,1<(1-
)α+
<α,
…1<(1-
)α+
<α,
将以上不等式相加得:n<
(1-
)α+
<nα,
即1<
((
)α+
)<α.
若切点为原点,由f′(0)=α知切线方程为y=αx+1;
若切点不为原点,设切点为(x0,(1+x0)α),
∴由切线过原点可知
| (1+x0)α |
| x0 |
| 1 |
| α-1 |
∵f′(
| 1 |
| α-1 |
| αα |
| (α-1)α-1 |
∴切线方程为y=
| αα |
| (α-1)α-1 |
| α |
| α-1 |
综上,所求切线有两条:y=αx+1和y=
| αα |
| (α-1)α-1 |
| α |
| α-1 |
(2)令g(x)=f(x)-1-αx-Ax2,则g(0)=0,g′(x)=α(1+x)α-1-α-2Ax,
显然g′(0)=0,且g′(x)的导函数为g″(x)=α(α-1)(1+x)α-2-2A.
若A≤
| α(α-1) |
| 2 |
| 2A |
| α(α-1) |
即g′(x)在(0,+∞)上单调增,从而g′(x)>g′(0)=0对x>0恒成立,从而g(x)在(0,+∞)单调增,
∴g(x)>g(0)=0对x>0恒成立.
若A>
| α(α-1) |
| 2 |
| 2A |
| α(α-1) |
| 2A |
| α(α-1) |
由g′(0)=0知存在x1>0,使得g′(x)<0对x∈(0,x1)恒成立,
∵g(0)=0,∴g(x)>0不能对x>0恒成立,
综上,最大实数A是
| α(α-1) |
| 2 |
(3)证明:当α>1时,令h(x)=f(x)-αx,则h′(x)=α[(1+x)α-1-1],
∴x∈(-1,0)时,h′(x)<0,
即h(x)=f(x)-αx在[-1,0]上单调递减,∴h(0)<h(x)<h(-1)对x∈(-1,0)恒成立,
∵h(0)=1,h(-1)=α,
∴1<h(x)<α,
即对x∈(-1,0)恒有1<(1+x)α-αx<α,
在此不等式中x=-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
∴1<(1-
| 1 |
| 2 |
| α |
| 2 |
| 1 |
| 3 |
| α |
| 3 |
| 1 |
| 4 |
| α |
| 4 |
| 1 |
| 5 |
| α |
| 5 |
…1<(1-
| 1 |
| n+1 |
| α |
| n+1 |
将以上不等式相加得:n<
| n+1 |
 |
| k=2 |
| 1 |
| k |
| α |
| k |
即1<
| 1 |
| n |
| n+1 |
 |
| k=2 |
| k-1 |
| k |
| α |
| k |
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性,考查不等式的证明,正确构造函数是关键.

练习册系列答案
相关题目
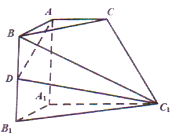 如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.
如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.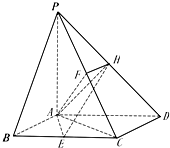 如图,四棱锥P-ABCD的底面是菱形,∠ABC=60°,PA⊥底面ABCD,E,F分别是BC,PC的中点,点H在PD上,且EH⊥PD,PA=AB=2.
如图,四棱锥P-ABCD的底面是菱形,∠ABC=60°,PA⊥底面ABCD,E,F分别是BC,PC的中点,点H在PD上,且EH⊥PD,PA=AB=2.