Question

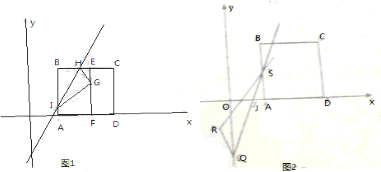
球O的直径SC=4，A，B是该球球面上的两点，AB=2，∠ASC=∠BSC=

π

4

，则棱锥A-SBC的体积为（　　）

• A、

  4

  3

• B、

  8

  3

• C、

  4 2

  3

• D、

  4 3

  3

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：由题意知，在棱锥S-ABC中，△SAC，△SBC都是等腰直角三角形，SC垂直于面ABD，棱锥S-ABC的体积为两个棱锥S-ABD和C-ABD的体积和．

解答： 解：∵球O的直径SC=4，A，B是该球球面上的两点，
AB=2，∠ASC=∠BSC=

π

4

，
∴由题意知，在棱锥S-ABC中，
△SAC，△SBC都是等腰直角三角形，其中AB=2，SC=4，
SA=AC=SB=BC=2

2

．
取SC的中点D，则AD⊥SC，BD⊥SC，
∴SC垂直于面ABD，
∴棱锥S-ABC的体积为两个棱锥S-ABD和C-ABD的体积和，
∴棱锥S-ABC的体积V=

1

3

SC•S_△ADB=

1

3

×4×

3

=

4 3

3

．
故选：D．

点评：本题考查棱锥的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．