题目内容
已知函数f(x)=
.
(1)已知sinα=
,求f(α)的值;
(2)已知tanα=-
且0<α<π,求f(2α+
)的值.
| sin2x+2sin2x | ||
sin(x+
|
(1)已知sinα=
| 1 |
| 3 |
(2)已知tanα=-
| 3 |
| 4 |
| π |
| 6 |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:(1)分子提取2sinx后,约分化简原式后代入即可求值;
(2)先求得sin2α,cos2α的值,用二倍角的正弦、余弦公式化简f(2α+
)后代入即可求值.
(2)先求得sin2α,cos2α的值,用二倍角的正弦、余弦公式化简f(2α+
| π |
| 6 |
解答:
解:(1)∵sinα=
,
∴f(α)=
=
=2
sinα=
.
(2)∵tanα=-
且0<α<π,
∴sin2α=
=-
,cos2α=
=
,
∴f(2α+
)=
=
=2
sin(2α+
)=2
(sin2α×
+
×cos2α)=
.
| 1 |
| 3 |
∴f(α)=
| 2sinαcosα+2sin2α | ||||
|
| 2sinα(cosα+sinα) | ||||
|
| 2 |
2
| ||
| 3 |
(2)∵tanα=-
| 3 |
| 4 |
∴sin2α=
| 2tanα |
| 1+tan2α |
| 24 |
| 25 |
| 1-tan2α |
| 1+tan2α |
| 7 |
| 25 |
∴f(2α+
| π |
| 6 |
sin(4α+
| ||||
sin(2α+
|
2sin(2α+
| ||||||||
|
| 2 |
| π |
| 6 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
7
| ||||
| 25 |
点评:本题主要考察了二倍角的正弦、余弦公式的应用,三角函数中的恒等变换应用,计算量比较大,要认真细心,属于基本知识的考查.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
球O的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=
,则棱锥A-SBC的体积为( )
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
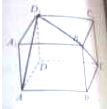 如图,已知ABCD-A1B1C1D1为正方体.
如图,已知ABCD-A1B1C1D1为正方体.