题目内容
设数列{an}是公差大于零的等差数列,已知a1=2,a3=a22-10.
(1)求{an}的通项公式;
(2)设数列{bn}是以函数f(x)=4sin2πx的最小正周期为首项,以3为公比的等比数列,求数列{an•bn}的前n项和Sn.
(1)求{an}的通项公式;
(2)设数列{bn}是以函数f(x)=4sin2πx的最小正周期为首项,以3为公比的等比数列,求数列{an•bn}的前n项和Sn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件,利用等差数列的通项公式列出方程组,求出等差数列的首项和公差,由此能求出{an}的通项公式.
(2)由已知条件利用三角函数求出数列{bn}首项为1从而bn=3n-1,得到an•bn=2n•3n-1,由此利用错位相减法能求出数列{an•bn}的前n项和Sn.
(2)由已知条件利用三角函数求出数列{bn}首项为1从而bn=3n-1,得到an•bn=2n•3n-1,由此利用错位相减法能求出数列{an•bn}的前n项和Sn.
解答:
解:(1)设{an}的公差为d,d>0,
∵a1=2,a3=a22-10,
∴
,解得a=2或d=-4(舍).(5分)
∴an=2+(n-1)×2=2n.(6分)
(2)∵y=4sin2πx=4×
=-2cos2πx+2,
其最小正周期为
=1,
∴首项为b1=1.(7分)
∵公比为q=3,从而bn=3n-1,
∴an•bn=2n•3n-1,(8分)
∴Sn=2•30+4•3+6•32+…+2n•3n-1,①
3Sn=2•3+4•32+6•33+…+2n•3n,②
①-②,得:-2Sn=2+2(3+32+33+…+3n-1)-2n•3n
=2+2×
-2n•3n
=2+3n-3-2n•3n,
∴Sn=
.(12分)
∵a1=2,a3=a22-10,
∴
|
∴an=2+(n-1)×2=2n.(6分)
(2)∵y=4sin2πx=4×
| 1-cos2πx |
| 2 |
=-2cos2πx+2,
其最小正周期为
| 2π |
| 2π |
∴首项为b1=1.(7分)
∵公比为q=3,从而bn=3n-1,
∴an•bn=2n•3n-1,(8分)
∴Sn=2•30+4•3+6•32+…+2n•3n-1,①
3Sn=2•3+4•32+6•33+…+2n•3n,②
①-②,得:-2Sn=2+2(3+32+33+…+3n-1)-2n•3n
=2+2×
| 3(1-3n-1) |
| 1-3 |
=2+3n-3-2n•3n,
∴Sn=
| (2n-1)•3n+1 |
| 2 |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
设
,
是两个非零向量,则使
•
=|
||
|成立的一个必要非充分条件是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列结论中,正确的是( )
| A、“?x∈Q,x2-5=0”的否定是假命题 |
| B、“?x∈R,x2+1<1”的否定是“?x∈R,x2+1<1” |
| C、“2≤2”是真命题 |
| D、“?x∈R,x2+1≠0”的否定是真命题 |
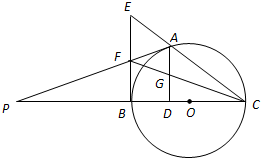 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.