题目内容
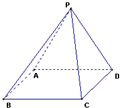如图，用四种不同的颜色给图中的P、A、B、C、D五个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂色方法共有（ ）种．| A、72 | B、86 |
| C、106 | D、120 |
考点：计数原理的应用
专题：排列组合
分析：根据分类计数原理，本题需要分两类，AC同色，和AC异色，问题得以解决，
解答：
解：当AC同色时，有
=48种，
当AC异色时，有
=24种，
根据分类计数原理得，不同的涂色方法共有48+24=72种．
故选：A．
| 2A | 3 4 |
当AC异色时，有
| A | 3 4 |
根据分类计数原理得，不同的涂色方法共有48+24=72种．
故选：A．
点评：本题考查了分类计数原理，关键是如何分类，属于中档题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知q是r的充分条件而不是必要条件，p是r的充分条件，s是r的必要条件，p是s的必要条件．现有下列命题：
①s是p的充要条件；
②r是p的必要条件而不是充分条件；
③q是p的充分条件而不是必要条件；
④r是s的充分条件而不是必要条件；
⑤?q是?s的必要条件而不是充分条件，
则正确命题序号是（ ）
①s是p的充要条件；
②r是p的必要条件而不是充分条件；
③q是p的充分条件而不是必要条件；
④r是s的充分条件而不是必要条件；
⑤?q是?s的必要条件而不是充分条件，
则正确命题序号是（ ）
| A、①③⑤ | B、①④⑤ |
| C、②③④ | D、③④⑤ |
已知i为虚数单位，复数
的共轭复数是（ ）
| 2 |
| 1-i |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
下列语句能使变量a的值为4的是（ ）
| A、INPUT a=4 |
| B、b=4，b=a |
| C、a=3，a=a+1 |
| D、2a=a+4 |
现有5名同学去听同时进行的6个课外知识讲座，每名同学可自由选择其中的一个讲座，不同选法的种数是（ ）
| A、54 | ||
| B、65 | ||
C、
| ||
| D、6×5×4×3×2 |
已知函数f（x）=x2+2bx的图象在点A（0，f（0））处的切线l与直线x-y+3=0平行，若数列{
}的前n项和为Sn，则S2011的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|