题目内容
如图，我国某搜救舰艇以30（海里/小时）的速度在南海某区域搜索，在点A处测得基地P在南偏东60°，向北航行40分钟后到达点B，测得基地P在南偏东30°，并发现在北偏东60°的航向上有疑似马航飘浮物，搜救舰艇立即转向直线前往，再航行80分钟到达飘浮物C处，求此时P、C间的距离．考点：解三角形的实际应用
专题：解三角形
分析：现根据题意求得AB，BC，进而根据∠A，∠ABP，∠APB利用正弦定理求得BP，最后利用勾股定理求得PC．
解答：
解：AB=30×
=20，BC=30×
=40．
在△ABP中，∠A=120°，∠ABP=30°，∠APB=30°，
∴BP=
•sin∠BAP=
sin120°=20
．
在Rt△BCP中，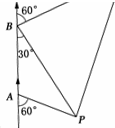
PC=
=
=20
．
∴P、C间的距离为20
（海里）．
| 40 |
| 60 |
| 80 |
| 60 |
在△ABP中，∠A=120°，∠ABP=30°，∠APB=30°，
∴BP=
| AB |
| sin∠APB |
| 20 |
| sin30° |
| 3 |
在Rt△BCP中，
PC=
| BC2+BP2 |
402+(20
|
| 7 |
∴P、C间的距离为20
| 7 |
点评：本题主要考查了解三角形的实际应用．解题的过程中注意利用三角形中的已知条件，利用正弦定理和余弦定理等基础知识来解决．
练习册系列答案
相关题目
现有5名同学去听同时进行的6个课外知识讲座，每名同学可自由选择其中的一个讲座，不同选法的种数是（ ）
| A、54 | ||
| B、65 | ||
C、
| ||
| D、6×5×4×3×2 |
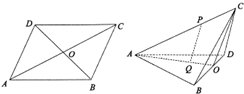如图，ABCD为边长2的菱形，∠BAD=60°，对角线交于点O，沿BD将BCD折起，使二面角C-BD-A为120°，P为折起后AC上一点，且AP=2PC，Q为△ABD的中心．