题目内容
用”辗转相除法”求得98与63的最大公约数是（ ）
| A、17 | B、14 | C、9 | D、7 |
考点：用辗转相除计算最大公约数
专题：算法和程序框图
分析：利用“辗转相除法”即可得出．
解答：
解：∵98=63×1+35，63=35×1+28，35=28×1+7，28=7×4．
∴98与63的最大公约数是7．
故选：D．
∴98与63的最大公约数是7．
故选：D．
点评：本题考查了“辗转相除法”，属于基础题．
练习册系列答案
相关题目
某校150名教职工中，有老年人20个，中年人50个，青年人80个，从中抽取30个作为样本．
①采用随机抽样法：抽签取出30个样本；
②采用系统抽样法：将教工编号为00，01，…，149，然后平均分组抽取30个样本；
③采用分层抽样法：从老年人，中年人，青年人中抽取30个样本．
下列说法中正确的是（ ）
①采用随机抽样法：抽签取出30个样本；
②采用系统抽样法：将教工编号为00，01，…，149，然后平均分组抽取30个样本；
③采用分层抽样法：从老年人，中年人，青年人中抽取30个样本．
下列说法中正确的是（ ）
| A、无论采用哪种方法，这150个教工中每一个被抽到的概率都相等 |
| B、①②两种抽样方法，这150个教工中每一个被抽到的概率都相等；③并非如此 |
| C、①③两种抽样方法，这150个教工中每一个被抽到的概率都相等；②并非如此 |
| D、采用不同的抽样方法，这150个教工中每一个被抽到的概率是各不相同的 |
极坐标系中，过点（2，
）且与极轴垂直的直线方程为（ ）
| π |
| 3 |
A、ρsinθ=-
| ||
B、ρ=-
| ||
| C、ρ=-4cosθ | ||
| D、ρcosθ-1=0 |
已知集合M={x|
＞0}，N={x|-3x2+x+2＞0}，则M∩N=（ ）
| 2x-1 |
| x+1 |
| A、（-∞，-1）∪（1，+∞） | ||
B、（
| ||
| C、（1，+∞） | ||
D、（-∞，-1）∪（-
|
曲线y=x3+x-2上点P0处的切线斜率为4，则点P0的一个坐标是（ ）
| A、（0，-2） |
| B、（1，1） |
| C、（-1，-4） |
| D、（1，4） |
现有5名同学去听同时进行的6个课外知识讲座，每名同学可自由选择其中的一个讲座，不同选法的种数是（ ）
| A、54 | ||
| B、65 | ||
C、
| ||
| D、6×5×4×3×2 |
函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分图象如图所示，则（ ）
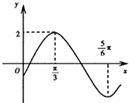
| π |
| 2 |
A、ω=1，φ=
| ||
B、ω=1，φ=-
| ||
C、ω=2，φ=
| ||
D、ω=2，φ=-
|
如图，在三棱锥P-ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．PC=1，BC=1．