题目内容
已知抛物线y2=4x，倾斜角为45°的直线l过抛物线的焦点，且与抛物线交于A、B两点，求线段AB的长度．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先根据题意给出直线l的方程，代入抛物线，求出两交点的横坐标的和，然后利用焦半径公式求解即可．
解答：
解：由y2=4x得焦点为F（1，0），所以直线l：y=x-1，
代入抛物线y2=4x化简得x2-6x+1=0，
设A（x1，y1），B（x2，y2），则x1+x2=6，
所以|AB|=x1+x2+p=6+2=8．
故所求的弦长为8．
代入抛物线y2=4x化简得x2-6x+1=0，
设A（x1，y1），B（x2，y2），则x1+x2=6，
所以|AB|=x1+x2+p=6+2=8．
故所求的弦长为8．
点评：本题考查了直线与抛物线的位置关系中的弦长问题，因为是过焦点的弦长问题，所以利用了焦半径公式．属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
记集合M={x|x＞2}，N={x|x2-3x≤0}，则M∩N=（ ）
| A、{x|2＜x≤3} |
| B、{x|x＞0或x＜-2} |
| C、{x|-2＜x≤3} |
| D、{x|0＜x＜2} |
已知在正方体ABCD-A1B1C1D1中，l?平面A1B1C1D1，且l与B1C1不平行，则下列一定不可能的是（ ）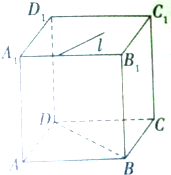
| A、l与AD平行 |
| B、l与AB异面 |
| C、l与CD所成角为30° |
| D、l与BD垂直 |
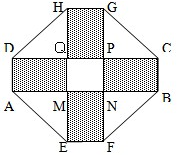某小区要建一座八边形的休闲公园，它的主体造型的平面图是由两个相同的举行ABCD和EFGH构成的面积为200m2的十字型地域，计划在正方形MNPQ上建一座花坛，造价为4200元/m2，在四个相同的矩形上（途中阴影部分）铺花岗岩地坪，造价为210元/m2，再在四个角上铺草坪，造价为80元/m2．受地域影响，AD的长最多能达到2