题目内容
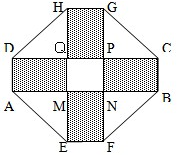某小区要建一座八边形的休闲公园，它的主体造型的平面图是由两个相同的举行ABCD和EFGH构成的面积为200m2的十字型地域，计划在正方形MNPQ上建一座花坛，造价为4200元/m2，在四个相同的矩形上（途中阴影部分）铺花岗岩地坪，造价为210元/m2，再在四个角上铺草坪，造价为80元/m2．受地域影响，AD的长最多能达到2| 3 |
（1）设总造价为S元，AD的长为xm，试建立S关于x的函数关系式；
（2）当x取何值时，S最小，并求出这个最小值．
考点：根据实际问题选择函数类型
专题：计算题,应用题,函数的性质及应用,不等式的解法及应用
分析：（1）由题意先求出边长AM，从而写出S关于x的函数关系式；
（2）利用基本不等式求最值，注意等号是否成立．
（2）利用基本不等式求最值，注意等号是否成立．
解答：
解：（1）设AM=z，则4zx+x2=200，
则z=
；
则S=4200x2+210×（200-x2）+80×2×
×
=4000（x2+
）+38000，（0＜x≤2
）；
（2）∵x2+
≥20，
（当且仅当x2=
，即x=
时，等号成立）
∴当x=
m时，S最小，
最小值为4000×20+38000=118000（元）．
则z=
| 200-x2 |
| 4x |
则S=4200x2+210×（200-x2）+80×2×
| 200-x2 |
| 4x |
| 200-x2 |
| 4x |
=4000（x2+
| 100 |
| x2 |
| 3 |
（2）∵x2+
| 100 |
| x2 |
（当且仅当x2=
| 100 |
| x2 |
| 10 |
∴当x=
| 10 |
最小值为4000×20+38000=118000（元）．
点评：本题考查了实际问题转化为数学问题的能力及基本不等式的应用，属于中档题．
练习册系列答案
相关题目
设全集U={x|x≥0}，集合P={1}，则∁UP=（ ）
| A、[0，1）∪（1，+∞） |
| B、（-∞，1） |
| C、（-∞，1）∪（1，+∞） |
| D、（1，+∞） |
用min{a，b}表示a，b两数中的最小值，函数f（x）=min{|2x|，|2x+t|}的图象关于直线x=-1对称，若方程f（x）=m恰有4个不相等的实数根，则实数m的取值范围为（ ）
| A、（0，1] |
| B、（0，1） |
| C、（0，2] |
| D、（0，2） |