题目内容
甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为
,乙投进的概率为
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
| 4 |
| 5 |
| 1 |
| 2 |
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(1)根据相互独立事件的概率乘法公式求得甲投进2球的概率、乙投进1球的概率,再把这两个概率相乘,即为所求.
(2)在甲第一次投篮未进的条件下,甲获胜,指甲后两投两进且乙三投一进或零进(记为A),或甲后两投一进且乙三投零进(记为B),分别根据相互独立事件的概率乘法公式求得P(A)和P(B),则甲最终获胜的概率为P(A)+P(B).
(2)在甲第一次投篮未进的条件下,甲获胜,指甲后两投两进且乙三投一进或零进(记为A),或甲后两投一进且乙三投零进(记为B),分别根据相互独立事件的概率乘法公式求得P(A)和P(B),则甲最终获胜的概率为P(A)+P(B).
解答:
解:(1)甲投进2球的概率为
•(
)2•
=
,乙投进1球的概率为
•
•(
)2=
,
甲投进2球且乙投进1球的概率为
×
=
.
(2)在甲第一次投篮未进的条件下,甲获胜,指甲后两投两进且乙三投一进或零进(记为A),或甲后两投一进且乙三投零进(记为B),
P(A)=
•(
)2•[
•
•(
)2+
(
)3]=
,P(B)=
•
•
•
(
)3=
,
∴甲最终获胜的概率为P(A)+P(B)=
.
| C | 2 3 |
| 4 |
| 5 |
| 1 |
| 5 |
| 48 |
| 125 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
甲投进2球且乙投进1球的概率为
| 48 |
| 125 |
| 3 |
| 8 |
| 18 |
| 125 |
(2)在甲第一次投篮未进的条件下,甲获胜,指甲后两投两进且乙三投一进或零进(记为A),或甲后两投一进且乙三投零进(记为B),
P(A)=
| C | 2 2 |
| 4 |
| 5 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 0 3 |
| 1 |
| 2 |
| 8 |
| 25 |
| C | 1 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 25 |
∴甲最终获胜的概率为P(A)+P(B)=
| 9 |
| 25 |
点评:本题主要考查相互独立事件的概率乘法公式,互斥事件的概率加法公式,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x.若在区间[-2,2]上方程ax+a-f(x)=0恰有三个不相等的实数根,则实数a的取值范围是( )
| A、[0,1) |
| B、[0,2] |
| C、[1,+∞) |
| D、[2,+∞) |
已知a,b是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A、若a∥b,b?α,则a∥α |
| B、若a∥α,b?α,则a∥b |
| C、若a⊥α,b⊥α,则a∥b |
| D、若a⊥b,b⊥α,则a∥α |
设函数f(x)=log3
-a在(1,2)内有零点,则实数a的取值范围是( )
| x+2 |
| x |
| A、(0,log32) |
| B、(log32,1) |
| C、(-1,-log32) |
| D、(1,log34) |
下列各组中的两个函数是同一函数的为( )
(1)y=
,y=x-5;
(2)y=
,y=
;
(3)y=|x|,y=
;
(4)y=x,y=
;
(5)y=(2x-5)2,y=|2x-5|.
(1)y=
| (x+3)(x-5) |
| x+3 |
(2)y=
| x+1 |
| x-1 |
| (x+1)(x-1) |
(3)y=|x|,y=
| x2 |
(4)y=x,y=
| 3 | x3 |
(5)y=(2x-5)2,y=|2x-5|.
| A、(1),(2) |
| B、(2),(3) |
| C、(3),(5) |
| D、(3),(4) |
已知集合A={x|-1<x<3},B={x|log2x<2},则A∩B=( )
| A、(-1,3) |
| B、(0,4) |
| C、(0,3) |
| D、(-1,4) |
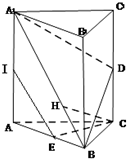 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.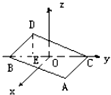 如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(
如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(