Question

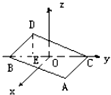 如图，在空间直角坐标系中，BC=2，原点O是BC的中点，点A的坐标是（

3

2

，

1

2

，0），点D在平面yOz上，且∠BDC=90°，∠DCB=30°，求点D的坐标．

Answer 1

考点：空间中的点的坐标

专题：空间位置关系与距离

分析：由题意求出OE，DE，即可得到D的坐标．

解答： 解：过D作DE⊥BC，垂足为E，在Rt△BDC中，∠BDC=90°，∠DCB=30°，BC=2，
得BD=1，CD=

3

，
DE=CDsin30°=

3

2

，
OE=OB-BE=OB-BDcos60°=1-

1

2

=

1

2

．
∴点D的坐标（0，-

1

2

，

3

2

）．

点评：本题考查空间的点的坐标的求法，基本知识的考查．