题目内容
已知定义域为R的函数f(x)=
是奇函数.
(1)求a,b的值;
(2)用定义域证明f(x)在(-∞,+∞)上为减函数;
(3)若对于t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的范围.
| b-2x |
| 2x+a |
(1)求a,b的值;
(2)用定义域证明f(x)在(-∞,+∞)上为减函数;
(3)若对于t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的范围.
考点:函数恒成立问题,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:第(1)问,由奇函数的定义,f(-x)=-f(x)恒成立,构造关于a、b的方程组,解出a、b即可;
第(2)问,按照取值、作差、判断符号、下结论三步完成单调性的证明;
第(3)问,将f(t2-2t)+f(2t2-k)<0移项得f(t2-2t)<-f(2t2-k),再利用奇偶性变形为f(t2-2t)<f(-2t2+k),最后利用单调性、定义域构造关于t的不等式恒成立,然后通过将k分离,最终化为函数的最值问题.
第(2)问,按照取值、作差、判断符号、下结论三步完成单调性的证明;
第(3)问,将f(t2-2t)+f(2t2-k)<0移项得f(t2-2t)<-f(2t2-k),再利用奇偶性变形为f(t2-2t)<f(-2t2+k),最后利用单调性、定义域构造关于t的不等式恒成立,然后通过将k分离,最终化为函数的最值问题.
解答:
解:(1)∵函数f(x)=
是奇函数,
∴f(-x)=-f(x)恒成立,
即f(-x)=
=
=-
=
恒成立,
即
=
恒成立,
∴a=b=1.
(2)证明:任取x1<x2,
则f(x1)-f(x2)=
-
=
①,
∵函数y=2x在R内是增函数,且x1<x2,
∴2x1<2x2,∴2x2-2x1>0,
又2x1+1>0,2x2+1>0,
∴①式>0,
∴f(x1)-f(x2)>0
∴f(x1)>f(x2),
∴函数f(x)=
在(-∞,+∞)上为减函数.
(3)f(t2-2t)+f(2t2-k)<0可化为
f(t2-2t)<-f(2t2-k),∵f(x)是奇函数,
∴f(t2-2t)<f(-2t2+k),又∵在R上f(x)是减函数,
∴t2-2t>-2t2+k恒成立,
即k<3t2-2t,t∈R恒成立,
只需k<(3(t-
) 2-
)min=-
,
∴k的取值范围是(-∞,-
).
| b-2x |
| 2x+a |
∴f(-x)=-f(x)恒成立,
即f(-x)=
| b-2-x |
| 2-x+a |
| b•2x-1 |
| a•2x+1 |
| b-2x |
| 2x+a |
| 2x-b |
| 2x+a |
即
| b•2x-1 |
| a•2x+1 |
| 2x-b |
| 2x+a |
∴a=b=1.
(2)证明:任取x1<x2,
则f(x1)-f(x2)=
| 1-2x1 |
| 2x1+1 |
| 1-2x2 |
| 2x2+1 |
| 2(2x2-2x1) |
| (2x1+1)(2x2+1) |
∵函数y=2x在R内是增函数,且x1<x2,
∴2x1<2x2,∴2x2-2x1>0,
又2x1+1>0,2x2+1>0,
∴①式>0,
∴f(x1)-f(x2)>0
∴f(x1)>f(x2),
∴函数f(x)=
| b-2x |
| 2x+a |
(3)f(t2-2t)+f(2t2-k)<0可化为
f(t2-2t)<-f(2t2-k),∵f(x)是奇函数,
∴f(t2-2t)<f(-2t2+k),又∵在R上f(x)是减函数,
∴t2-2t>-2t2+k恒成立,
即k<3t2-2t,t∈R恒成立,
只需k<(3(t-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴k的取值范围是(-∞,-
| 1 |
| 3 |
点评:研究函数的性质,必须遵循定义域优先的原则;函数的奇偶性定义式是一个恒等式,利用这一点,f(-x)化简后与-f(x)是关于x的同一个式子,由此得到关于系数的方程;利用定义证明函数的单调性,关键是第二步作差,一般是将差变形为能够直接判断符号的式子,比如分解因式、化为常数、完全平方式等等.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
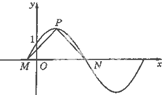 如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
等差数列{an},{bn}的前n项和分别为Sn,Tn,若
=
,则an=bn时n=( )
| Sn |
| Tn |
| 2n+4 |
| 3n+1 |
| A、无解 | B、6 | C、2 | D、无数多个 |

