题目内容
9. 如图,已知平面DBC与直线PA均垂直于三角形ABC所在平面,
如图,已知平面DBC与直线PA均垂直于三角形ABC所在平面,(1)求证:PA∥平面DBC;
(2)若AD⊥BC,求证:平面DBC⊥平面PAD.
分析 (1)过点D作DO⊥BC,交BC于O,则DO⊥平面ABC,从而PA∥DO,由此能证明PA∥平面DBC.
(2)推导出BC⊥PA,AD⊥BC,从而BC⊥平面PAD,由此能证明平面DBC⊥平面PAD.
解答 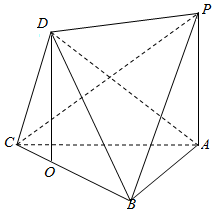 证明:(1)在△BDC中,过点D作DO⊥BC,交BC于O,
证明:(1)在△BDC中,过点D作DO⊥BC,交BC于O,
∵平面DBC与直线PA均垂直于三角形ABC所在平面,
∴DO⊥平面ABC,∴PA∥DO,
∵PA?平面DBC,DO?平面DBC,
∴PA∥平面DBC.
解:(2)∵直线PA⊥平面ABC,BC?平面ABC,
∴BC⊥PA,
∵AD⊥BC,AD∩PA=A,
∴BC⊥平面PAD,
∵BC?平面DBC,
∴平面DBC⊥平面PAD.
点评 本题考查线面平行的证明,考查面面垂直的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
4.在空间,下列命题中正确的是( )
| A. | 没有公共点的两条直线平行 | B. | 与同一直线垂直的两条直线平行 | ||
| C. | 垂直于同一平面的两条直线平行 | D. | 若直线a不在平面α内,则a∥平面α |
14.已知正方形的边长为1,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{BC}=\overrightarrow b,\overrightarrow{AC}=\overrightarrow c$,则$|{\overrightarrow a+\overrightarrow b+\overrightarrow c}|$等于( )
| A. | 0 | B. | 3 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
19.将y=cosx的图象上的所有点的纵坐标不变,横坐标缩小到原来的一半,然后再将所得图象向左平移$\frac{π}{4}$个单位长度,则最后所得图象的解析式为( )
| A. | y=cos(2x+$\frac{π}{4}$) | B. | y=cos($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=sin2x | D. | y=-sin2x |
 如图,矩形AB′DE(AE=6,DE=5),被截去一角(即△BB′C),AB=3,∠ABC=135°,平面PAE⊥平面ABCDE,PA+PE=10.
如图,矩形AB′DE(AE=6,DE=5),被截去一角(即△BB′C),AB=3,∠ABC=135°,平面PAE⊥平面ABCDE,PA+PE=10.