题目内容
已知数列{an}中,a1≠0,2an=a1(1+Sn)(n∈N*),Sn为数列{an}的前n项和.
(1)求数列{an}的通项公式an;
(2)设bn=nSn,求数列{bn}的前n项和为Tn.
(1)求数列{an}的通项公式an;
(2)设bn=nSn,求数列{bn}的前n项和为Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出a1=1,2an-2an-1=(1+Sn)-(1+Sn-1)=an,由此得到an=2n-1.
(2)由an=2n-1,得Sn=2n-1,从而bn=n×2n-n,由此利用公组求和法能求出数列{bn}的前n项和为Tn.
(2)由an=2n-1,得Sn=2n-1,从而bn=n×2n-n,由此利用公组求和法能求出数列{bn}的前n项和为Tn.
解答:
解:(1)∵数列{an}中,a1≠0,2an=a1(1+Sn)(n∈N*),
当n=1时,2a1=a1(1+S1)=a1(1+a1),
∵a1≠0,∴a1=1,
当n>1时,则2an=1+Sn,
∴2an-2an-1=(1+Sn)-(1+Sn-1)=an,∴an=2an-1,
∴{an}是首项a1=1、公比q=2等比数列,
∴an=2n-1.…(6分)
(2)由(1)得an=2n-1,
Sn为数列{an}的前n项和,
Sn=
,
∴Sn=2n-1,
∴bn=n×2n-n,…(7分)
∴Tn=(n-1)×2n+1+2-
.…(12分)
当n=1时,2a1=a1(1+S1)=a1(1+a1),
∵a1≠0,∴a1=1,
当n>1时,则2an=1+Sn,
∴2an-2an-1=(1+Sn)-(1+Sn-1)=an,∴an=2an-1,
∴{an}是首项a1=1、公比q=2等比数列,
∴an=2n-1.…(6分)
(2)由(1)得an=2n-1,
Sn为数列{an}的前n项和,
Sn=
| 1-2n |
| 1-2 |
∴Sn=2n-1,
∴bn=n×2n-n,…(7分)
∴Tn=(n-1)×2n+1+2-
| n(n+1) |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
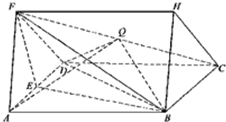 如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上.
如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上.