题目内容
已知函数f(x)=x2-(k+1)2x+1,若存在x1∈[k,k+1],x2∈[k+2,k+4],使得f(x1)=f(x2),则实数k的取值范围为( )
A、[-
| ||||||||
B、[-
| ||||||||
| C、[-2,-1]∪[1,2] | ||||||||
D、[-
|
考点:二次函数的性质
专题:函数的性质及应用
分析:由函数的表达式求出函数的对称轴,由函数的对称性得到不等式组,解不等式组求出即可.
解答:
解:由题意得:对称轴x=
,
又f(x1)=f(x2),
∴
≤
≤
,
解得:-2≤k≤-1,1≤k≤2,
故答案选;C.
| (k+1)2 |
| 2 |
又f(x1)=f(x2),
∴
| 2k+2 |
| 2 |
| k+12 |
| 2 |
| 2k+5 |
| 2 |
解得:-2≤k≤-1,1≤k≤2,
故答案选;C.
点评:本题考察了二次函数的性质,主要是二次函数的对称性,对称轴的求法以及解不等式组,属于中难度题.

练习册系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=3x+2y的最大值为( )
|
| A、10 | B、8 | C、7 | D、2 |
已知M(1,2),N(4,3)直线l过点P(2,-1)且与线段MN相交,那么直线l的斜率k的取值范围是( )
| A、(-∞,-3]∪[2,+∞) | ||||
B、[-
| ||||
| C、[-3,2] | ||||
D、(-∞,-
|
函数y=
cos2x+sinxcosx(-
)的周期是( )
| 3 |
| ||
| 2 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
复数z=-2+i,则它的共轭复数
在复平面内对应的点位于( )
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
“x≥1”是“x+
≥2”( )
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分且必要条件 |
| D、既不充分也不必要条件 |

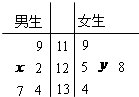 某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.
某数学兴趣小组有男女生各5名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为125,女生数据的平均数为126.8.