题目内容
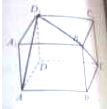如图，已知ABCD-A1B1C1D1为正方体．（1）求AD1与B1B所成的角的大小．
（2）与AD1异面，且与AD1所成角是45°的正方体的棱有哪几条？
（3）求AD1与B1C所成的角的大小．
（4）如果MN分别是B1C1，C1C的中点，求MN与AD1所成角的大小．
考点：异面直线及其所成的角
专题：空间位置关系与距离,空间角
分析：（1）由AA1∥B1B，得∠A1AD1是AD1与B1B所成的角，由此能求出AD1与B1B所成的角的大小．
（2）与AD1异面，且与AD1所成角是45°的正方体的棱有4条．
（3）由B1C∥A1D，AD1⊥A1D，能求出AD1与B1C所成的角的大小．
（4）MN∥B1C，又B1C∥A1D，AD1⊥A1D，由此能求出MN与AD1所成角的大小．
（2）与AD1异面，且与AD1所成角是45°的正方体的棱有4条．
（3）由B1C∥A1D，AD1⊥A1D，能求出AD1与B1C所成的角的大小．
（4）MN∥B1C，又B1C∥A1D，AD1⊥A1D，由此能求出MN与AD1所成角的大小．
解答：
解：（1）∵AA1∥B1B，
∴∠A1AD1是AD1与B1B所成的角，
∵∠A1AD1=45°，
∴AD1与B1B所成的角为45°．
（2）与AD1异面，且与AD1所成角是45°的正方体的棱有：
BB1，CC1，BC，B1C1，共4条．
（3）∵B1C∥A1D，
AD1⊥A1D，
∴AD1与B1C所成的角的大小为90°．
（4）∵M，N分别是B1C1，C1C的中点，
∴MN∥B1C，又B1C∥A1D，AD1⊥A1D，
∴MN与AD1所成角的大小为90°．
∴∠A1AD1是AD1与B1B所成的角，
∵∠A1AD1=45°，
∴AD1与B1B所成的角为45°．
（2）与AD1异面，且与AD1所成角是45°的正方体的棱有：
BB1，CC1，BC，B1C1，共4条．
（3）∵B1C∥A1D，
AD1⊥A1D，
∴AD1与B1C所成的角的大小为90°．
（4）∵M，N分别是B1C1，C1C的中点，
∴MN∥B1C，又B1C∥A1D，AD1⊥A1D，
∴MN与AD1所成角的大小为90°．
点评：本题考查空间角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
已知对任意实数x，有f（-x）=-f（x），且当x＞0时，有f′（x）＞0，则当x＜0时，有（ ）
| A、f'（x）≥0 |
| B、f'（x）＞0 |
| C、f'（x）≤0 |
| D、f'（x）＜0 |
若曲线y=f（x）在点（x0，f（x0））处的切线方程为3x+y+5=0，则（ ）
| A、f′（x0）＞0 |
| B、f′（x0）＜0 |
| C、f′（x）=0 |
| D、f′（x0）不存在 |
正三棱锥P-ABC中，∠APB=∠BPC=∠CPA=90°，PA=PB=PC=a，AB的中点M，一小蜜蜂沿锥体侧面由M 爬到C点，最短路程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某校高三某班的一次测试成绩的茎叶图、频率分布直方图及频率分布表中的部分数据如下，请据此解答如下问题：