题目内容
6．已知点A（1，0）和B（1，2）是圆x2+y2-2x-2y+1=0上的两点，若在直线y=kx-1上存在点P，使得$\overrightarrow{PA}$$•\overrightarrow{PB}$=0，则k的取值范围是（ ）| A． | k≥1 | B． | k≥$\frac{3}{4}$ | C． | k≤1 | D． | k≤$\frac{3}{4}$ |
分析 设点P（m，km-1），则由$\overrightarrow{PA}$$•\overrightarrow{PB}$=（k2+1）•m2-（4k+2）m+4=0，再根据它的判别式△≥0，求得k的范围．
解答 解：由于点A（1，0）和B（1，2），点P在直线y=kx-1上，可设点P（m，km-1），
则由$\overrightarrow{PA}$$•\overrightarrow{PB}$=（1-m 1-km）•（1-m 3-km）=（1-m）2+（1-km）（3-km）=（k2+1）•m2-（4k+2）m+4=0，
可得方程 （k2+1）•m2-（4k+2）m+4=0 有解，
故有△=（4k+2）2-4（k2+1）•4≥0，求得k≥$\frac{3}{4}$，
故选：B．
点评 本题主要考查直线和圆的位置关系，两个向量的数量积公式，属于中档题．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
16．设x0是方程log2x+x=0的根，则x0属于区间（ ）
| A． | （0，$\frac{1}{8}$） | B． | （$\frac{1}{8}$，$\frac{1}{4}$） | C． | （$\frac{1}{4}$，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，1） |
14．已知平面α和平面β相交，a是α内一条直线，则有（ ）
| A． | 在β内必存在与a平行的直线 | B． | 在β内必存在与a垂直的直线 | ||
| C． | 在β内不存在与a平行的直线 | D． | 在β内不一定存在与a垂直的直线 |
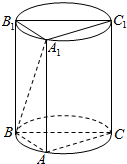如图，四边形BCC1B1是圆柱的轴截面．AA1是圆柱的一条母线，已知AB=4，AC=2$\sqrt{2}$，AA1=3．