Question

若关于x的方程sin2x+cos2x=k在区间[0，

π

2

]上有两个不同的实数解，则k的取值范围为

 

．

Answer 1

考点：两角和与差的正弦函数,三角函数的最值

专题：三角函数的图像与性质

分析：构造辅助函数f（x）=sin2x+cos2x，g（x）=k，求出f（x）在[0，

π

2

]上的值域并作出图象，
由两函数的图象有两个不同交点求得k的取值范围．

解答： 解：令f（x）=sin2x+cos2x，g（x）=k，
则f（x）=sin2x+cos2x
=

2

(

2

2

sin2x+

2

2

cos2x)=

2

sin(2x+

π

4

)．
∵x∈[0，

π

2

]，
∴2x+

π

4

∈[

π

4

，

5π

4

]，
∴

2

sin(2x+

π

4

)∈[-1，

2

]，
函数f（x）=

2

sin(2x+

π

4

)在[0，

π

2

]内的图象如图所示：

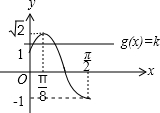
∴要使方程sin2x+cos2x=k在区间[0，

π

2

]上有两个不同的实数解，
则函数f（x）与g（x）的图象有两个不同的交点，
则k的取值范围为[1，

2

）．
故答案为：[1，

2

）．

点评：本题考查两角和与差的正弦函数，考查了三角函数最值的求法，训练了数学转化思想方法和数形结合的解题思想解题思想方法，是中档题．