题目内容
已知中心在坐标原点,焦点在y轴上的双曲线的渐近线方程为y=±
x,则此双曲线的离心率为( )
| 1 |
| 2 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由设双曲线方程为
-
=1,且
=
,由此能求出双曲线的离心率.
| y2 |
| a2 |
| x2 |
| b2 |
| a |
| b |
| 1 |
| 2 |
解答:
解:∵中心在坐标原点,焦点在y轴上的双曲线的渐近线方程为y=±
x,
∴设双曲线方程为
-
=1,且
=
,∴
=2,
∴e=
=
.
故选:D.
| 1 |
| 2 |
∴设双曲线方程为
| y2 |
| a2 |
| x2 |
| b2 |
| a |
| b |
| 1 |
| 2 |
| b |
| a |
∴e=
1+
|
| 5 |
故选:D.
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,注意双曲线的简单性质的合理运用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
在△ABC中,内角A,B,C的对边分别为a,b,c,已知acosB+bcosA=csinC,b2+c2-a2=
bc,则B=( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
任取一个三位正整数N,对数log2N是一个正整数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若集合M={x|y=
},N={x|y=
},则M∩N=( )
| x2-x3 |
2-(
|
| A、[-1,1] |
| B、[0,1] |
| C、(-∞,0]∪([1,+∞) |
| D、(-∞,-1]∪[1,+∞) |
已知全集U={0,1,2,3,4,5,6},集合A={1,2},B={0,2,5},则集合∁U(A∪B)=( )
| A、{0,1,2,5} |
| B、{2} |
| C、{0,1,3,4,5,6} |
| D、{3,4,6} |
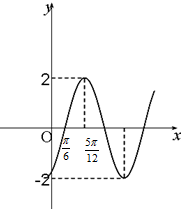 函数f(x)=2sin(ωx+φ),(ω>0,-
函数f(x)=2sin(ωx+φ),(ω>0,-| π |
| 2 |
| π |
| 2 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|
等差数列{an}中,a1=7,a3=3,前n项和为Sn,则n=( )时,Sn取到最大值.
| A、4或5 | B、4 | C、3 | D、2 |