题目内容
已知
，
，
均为单位向量，且满足
•
=0，则（
+
+
）•（
+
）的最大值为 ．
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| a |
| c |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由于
，
，
均为单位向量，满足
•
=0，可设
=（1，0），
=（0，1），
=（cosθ，sinθ）．利用向量的坐标运算和数量积运算、正弦函数的单调性即可得出．
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
解答：
解：∵
，
，
均为单位向量，满足
•
=0，
∴可设
=（1，0），
=（0，1），
=（cosθ，sinθ）．
∴（
+
+
）•（
+
）=（1+cosθ，1+sinθ）•（1+cosθ，sinθ）
=（1+cosθ）2+（1+sinθ）sinθ
=sinθ+2cosθ+2
=
sin(θ+φ）+2≤
+2，tanφ=2，当且仅当sin（θ+φ）=1时取等号．
∴（
+
+
）•（
+
）的最大值为
+2．
故答案为：
+2．
| a |
| b |
| c |
| a |
| b |
∴可设
| a |
| b |
| c |
∴（
| a |
| b |
| c |
| a |
| c |
=（1+cosθ）2+（1+sinθ）sinθ
=sinθ+2cosθ+2
=
| 5 |
| 5 |
∴（
| a |
| b |
| c |
| a |
| c |
| 5 |
故答案为：
| 5 |
点评：本题考查了向量的坐标运算和数量积运算、正弦函数的单调性，考查了计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
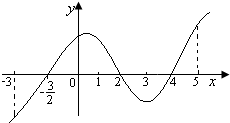如图是函数y=f（x）的导函数y=f′（x）的图象，对此图象，有如下结论：
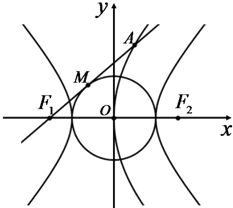如图，双曲线C1：