题目内容
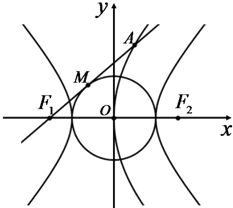 如图,双曲线C1:
如图,双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:根据题意,求出AF2的大小以及点A的坐标,又点A在抛物线C2:y2=4cx上,求出a、c的关系,从而得出离心率e的大小.
解答:
解:在△F1AF2中,MO为中位线,且F1M=b,OM=a,
∴AF2=2a;
由抛物线的定义,设A(x,y),
∴x+c=2a,
∴x=2a-c;
又∵点A到x轴的距离为
(由抛物线的定义,过点A做抛物线准线的垂线得到),
∴点A(2a-c,
);
∵点A在抛物线C2:y2=4cx上,
∴4b2-4a2=4c(2a-c),
即c2-2a2=c(2a-c),
∴c2-ac-a2=0,
∴e2-e-1=0;
又∵e>1,
∴解得e=
.
故选:A.
∴AF2=2a;
由抛物线的定义,设A(x,y),
∴x+c=2a,
∴x=2a-c;
又∵点A到x轴的距离为
| 4b2-4a2 |
∴点A(2a-c,
| 4b2-4a2 |
∵点A在抛物线C2:y2=4cx上,
∴4b2-4a2=4c(2a-c),
即c2-2a2=c(2a-c),
∴c2-ac-a2=0,
∴e2-e-1=0;
又∵e>1,
∴解得e=
1+
| ||
| 2 |
故选:A.
点评:本题考查了直线与圆,以及直线与圆锥曲线的应用问题,解题时应结合图形以及圆锥曲线的定义、几何性质进行解答,是综合题目.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
在△ABC中,A=45°,b=2
,c=1,则a=( )
| 2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、13 |
不等式x2≥2x的解集是( )
| A、{x|x≥2} |
| B、{x|x≤2} |
| C、{x|0≤x≤2} |
| D、{x|x≤0或x≥2} |
已知三次函数f(x)=
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
| 1 |
| 3 |
| A、m<2或m>4 |
| B、2≤m≤4 |
| C、2<m<4 |
| D、-4<m<-2 |
已知正项非常值数列{an},{bn}满足:an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列.令cn=
,则下列关于数列{cn}的说法正确的是( )
| bn |
| A、该数列为等差数列 |
| B、该数列为等比数列 |
| C、该数列的每一项为奇数 |
| D、该数列的每一项为偶数 |
在三棱柱ABC-A1B1C1中,已知AA1⊥平面ABC,AA1=2,BC=2
,∠BAC=
,此三棱柱各个顶点都在一个球面上,则球的体积为( )
| 3 |
| π |
| 2 |
A、
| ||
| B、16π | ||
C、
| ||
D、
|
已知数列{an}满足an+1=2an-an-1(n≥2),且a1=1,a2=2,则数列{
}的前10项之和等于( )
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|