题目内容
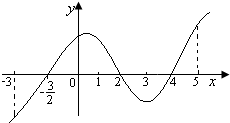 如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论:
如图是函数y=f(x)的导函数y=f′(x)的图象,对此图象,有如下结论:①在区间(-2,1)内f(x)是增函数;
②在区间(1,3)内f(x)是减函数;
③在x=2时,f(x)取得极大值;
④在x=3时,f(x)取得极小值.
其中正确的是
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的概念及应用
分析:先求出函数在各个区间上的导函数的符号,再分别对①②③④进行判断.
解答:
解:由 y=f'(x)的图象可知,
x∈(-3,-
),f'(x)<0,函数为减函数;
所以,①在区间(-2,1)内f(x)是增函数;不正确;
②在区间(1,3)内f(x)是减函数;不正确;
x=2时,y=f'(x)=0,且在x=2的两侧导数值先正后负,
③在x=2时,f(x)取得极大值;
而,x=3附近,导函数值为正,
所以,④在x=3时,f(x)取得极小值.不正确.
故答案为③.
x∈(-3,-
| 3 |
| 2 |
所以,①在区间(-2,1)内f(x)是增函数;不正确;
②在区间(1,3)内f(x)是减函数;不正确;
x=2时,y=f'(x)=0,且在x=2的两侧导数值先正后负,
③在x=2时,f(x)取得极大值;
而,x=3附近,导函数值为正,
所以,④在x=3时,f(x)取得极小值.不正确.
故答案为③.
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
在△ABC中,A=45°,b=2
,c=1,则a=( )
| 2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、13 |