题目内容
设函数f(x)=
sin
,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2,则m的取值范围是( )
| 3 |
| πx |
| m |
| A、(-∞,-6)∪(6,+∞) |
| B、(-∞,-4)∪(4,+∞) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-1)∪(1,+∞) |
考点:正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:由题意可得,f(x0)=±
,且
=kπ+
,k∈z,再由题意可得当m2最小时,|x0|最小,而|x0|最小为
|m|,可得m2 >
m2+3,由此求得m的取值范围.
| 3 |
| πx0 |
| m |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:由题意可得,f(x0)=±
,且
=kπ+
,k∈z,即 x0=
m.
再由x02+[f(x0)]2<m2,可得当m2最小时,|x0|最小,而|x0|最小为
|m|,
∴m2 >
m2+3,∴m2>4.
求得 m>2,或m<-2,
故选:C.
| 3 |
| πx0 |
| m |
| π |
| 2 |
| 2k+1 |
| 2 |
再由x02+[f(x0)]2<m2,可得当m2最小时,|x0|最小,而|x0|最小为
| 1 |
| 2 |
∴m2 >
| 1 |
| 4 |
求得 m>2,或m<-2,
故选:C.
点评:本题主要正弦函数的图象和性质,函数的零点的定义,体现了转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,角A、B、C所对应的边分别为a,b,c,则“a≤b”是“sinA≤sinB”的( )
| A、充分必要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
实部为-2,虚部为1的复数所对应的点位于复平面内的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设a,b是关于t的方程t2cosθ+tsinθ=0的两个不等实根,则过A(a,a2),B(b,b2)两点的直线与双曲线
-
=1的公共点的个数为( )
| x2 |
| cos2θ |
| y2 |
| sin2θ |
| A、0 | B、1 | C、2 | D、3 |
 设a是一个各位数字都不是0且没有重复数字三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=
设a是一个各位数字都不是0且没有重复数字三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=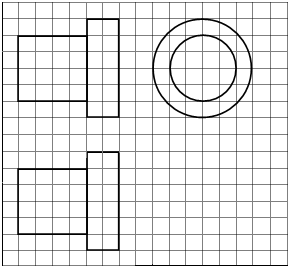 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )