题目内容
若tanα＞0，则（ ）
| A、sinα＞0 |
| B、cosα＞0 |
| C、sin2α＞0 |
| D、cos2α＞0 |
考点：三角函数值的符号
专题：三角函数的求值
分析：化切为弦，然后利用二倍角的正弦得答案．
解答：
解：∵tanα＞0，
∴
＞0，
则sin2α=2sinαcosα＞0．
故选：C．
∴
| sinα |
| cosα |
则sin2α=2sinαcosα＞0．
故选：C．
点评：本题考查三角函数值的符号，考查了二倍角的正弦公式，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设a是一个各位数字都不是0且没有重复数字三位数，将组成a的3个数字按从小到大排成的三位数记为I（a），按从大到小排成的三位数记为D（a）（例如a=815，则I（a）=158，D（a）=851），阅读如图所示的程序框图，运行相应的程序，任意输入一个a，输出的结果b=
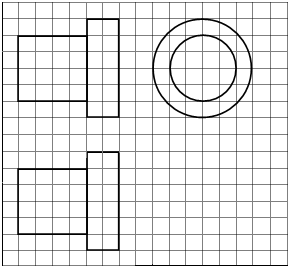如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
设F1，F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，双曲线上存在一点P使得|PF1|+|PF2|=3b，|PF1|•|PF2|=
ab，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 9 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
已知向量
=（1，2），
=（3，1），则
-
=（ ）
| a |
| b |
| b |
| a |
| A、（-2，1） |
| B、（2，-1） |
| C、（2，0） |
| D、（4，3） |