题目内容
已知过点P(1,-2),倾斜角为
的直线l和抛物线x2=y+m
(1)m取何值时,直线l和抛物线交于两点?
(2)m取何值时,直线l被抛物线截下的线段长为
.
| π |
| 6 |
(1)m取何值时,直线l和抛物线交于两点?
(2)m取何值时,直线l被抛物线截下的线段长为
4
| ||
| 3 |
考点:直线与圆锥曲线的关系
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由点斜式方程得到直线方程,联立抛物线方程,消去y,得到二次方程,由判别式大于0,解出即可;
(2)由(1)运用韦达定理,以及弦长公式,列方程,解出即可.
(2)由(1)运用韦达定理,以及弦长公式,列方程,解出即可.
解答:
解:(1)由已知可得直线l:y+2=
(x-1),
联立
得x2-
x+
+2-m=0,
因为有两个交点,所以△=
-4(
+2-m)>0,
解得m>
;
(2)设直线l交抛物线于A(x1,y1)、B(x2,y2)两点,
则x1+x2=
,x1x2=
+2-m,
则|AB|=
=
=
,
解得,m=
.
| ||
| 3 |
联立
|
| ||
| 3 |
| ||
| 3 |
因为有两个交点,所以△=
| 1 |
| 3 |
| ||
| 3 |
解得m>
23+4
| ||
| 12 |
(2)设直线l交抛物线于A(x1,y1)、B(x2,y2)两点,
则x1+x2=
| ||
| 3 |
| ||
| 3 |
则|AB|=
| (1+k2)((x1+x2)2-4x1x2 |
|
4
| ||
| 3 |
解得,m=
3
| ||
| 6 |
点评:本题考查抛物线的方程和运用,考查联立直线方程和抛物线方程,消去未知数,运用韦达定理和弦长公式解题,考查运算能力,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
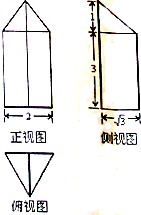

A、2
| ||||
B、4
| ||||
C、
| ||||
D、
|
函数f(x)=
,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
-2,e6+
-2)
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
|
①(1).m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈[e5+
| 1 |
| e |
| 1 |
| e2 |
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
球的半径为2,它的内接正方体的表面积为( )
| A、8 | B、16 | C、32 | D、64 |
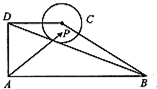 如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设
如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心,且与直线BD相切的圆内运动,设