Question

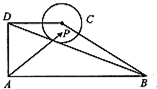如图，在直角梯形ABCD中，AB⊥AD，AD=DC=1，AB=3，动点P在以点C为圆心，且与直线BD相切的圆内运动，设

AP

=α

AD

+β

AB

（α，β∈R），则α+β的取值范围是

 

．

Answer 1

考点：平面向量的综合题

专题：平面向量及应用

分析：建立坐标系，转为三角函数：α+β=y+

x

3

=1+

1

10

sinθ+

1

3

+

1

3

（1+

1

10

cosθ）=

4

3

+

1

3 10

cosθ+

1

10

sinθ，利用三角变换公式求解．

解答： 解：以AB为x轴，以AD为y轴，建立坐标系，
∵在直角梯形ABCD中，AB⊥AD，AD=DC=1，AB=3
∴A（0，0），D（0，1），B（3，0），C（1，1）
∴直线BD的方程为：y=-

1

3

x+1，即x+3y-3=0，
C（1，1）点到直线的距离为：

10

10

∴以点C为圆心，且与直线BD相切的圆的方程为：
（x-1）²+（y-1）²=

1

10

，x=1+

1

10

cosθ，y=1+

1

10

sinθ
设P（x，y）则：（x-1）²+（y-1）²≤

1

10

，
∵

AP

=α

AD

+β

AB

，（α，β∈R），
∴（x，y）=（3β，α）
∴α+β=y+

x

3

=1+

1

10

sinθ+

1

3

+

1

3

（1+

1

10

cosθ）=

4

3

+

1

3 10

cosθ+

1

10

sinθ=

4

3

+

1

3

sin（θ+λ）
∵-

1

3

＜

1

3

sin（θ+λ）＜

1

3

，
1＜

4

3

+

1

3

sin（θ+λ）＜

5

3

，
∴α+β的取值范围是（1，

5

3

）
故答案为：(1，

5

3

)

点评：本题综合考查了向量与三角函数的运用，属于中档题．