题目内容
已知曲线C1:
(α为参数),曲线C2:ρsin(θ+
)=
,将C1的横坐标伸长为原来的2倍,纵坐标缩短为原来的
得到曲线C3.
(Ⅰ)求曲线C3的普通方程,曲线C2的直角坐标方程;
(Ⅱ)若点P为曲线C3上的任意一点,Q为曲线C2上的任意一点,求线段|PQ|的最小值,并求此时的P的坐标.
|
| π |
| 4 |
| 2 |
| 1 |
| 3 |
(Ⅰ)求曲线C3的普通方程,曲线C2的直角坐标方程;
(Ⅱ)若点P为曲线C3上的任意一点,Q为曲线C2上的任意一点,求线段|PQ|的最小值,并求此时的P的坐标.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(Ⅰ)通过变换求出曲线C3的参数方程然后求解它的普通方程,利用极坐标与直角坐标的关系,直接求解曲线C2的直角坐标方程;
(Ⅱ)点P为曲线C3上的任意一点,Q为曲线C2上的任意一点,线段|PQ|的最小值,转化为圆的圆心到直线的距离减去半径,利用直线的垂直关系,即可并求此时的P的坐标.
(Ⅱ)点P为曲线C3上的任意一点,Q为曲线C2上的任意一点,线段|PQ|的最小值,转化为圆的圆心到直线的距离减去半径,利用直线的垂直关系,即可并求此时的P的坐标.
解答:
(本题满分10分)
解:(Ⅰ)曲线C1:
(α为参数),将C1的横坐标伸长为原来的2倍,纵坐标缩短为原来的
得到曲线C3.
,∴曲线C3:x2+y2=1,
曲线C2:ρsin(θ+
)=
,即
ρsinθ+
ρcosθ=
,
∴曲线C2:x+y=2-----------(5分)
(II)设P(cosα,sinα),则线段|PQ|的最小值为点P到直线x+y=2的距离.
转化为圆的想到直线的距离减去半径,
∴|PQ|min=
-1=
-1,
直线x+y=2的斜率为-1,所以QP的斜率为1,P在x2+y2=1上,
所以p(
,
)-----------(10分)
解:(Ⅰ)曲线C1:
|
| 1 |
| 3 |
|
曲线C2:ρsin(θ+
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
∴曲线C2:x+y=2-----------(5分)
(II)设P(cosα,sinα),则线段|PQ|的最小值为点P到直线x+y=2的距离.
转化为圆的想到直线的距离减去半径,
∴|PQ|min=
| |0+0-2| | ||
|
| 2 |
直线x+y=2的斜率为-1,所以QP的斜率为1,P在x2+y2=1上,
所以p(
| ||
| 2 |
| ||
| 2 |
点评:本题考查直线的参数方程以及极坐标方程的应用点到直线的距离公式的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等差数列{an}中,已知a5+a7=10,Sn是{an}的前n项和,S11等于( )
| A、45 | B、50 | C、55 | D、60 |
 如图,圆周上有n个固定点,分别为A1,A2,…,An(n∈N*,n≥2),在每一个点上分别标上1,2,3中的某一个数字,但相邻的两个数字不相同,记所有的标法总数为an.
如图,圆周上有n个固定点,分别为A1,A2,…,An(n∈N*,n≥2),在每一个点上分别标上1,2,3中的某一个数字,但相邻的两个数字不相同,记所有的标法总数为an.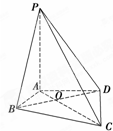 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.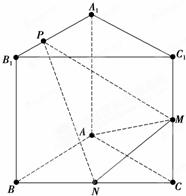 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2,
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2,