题目内容
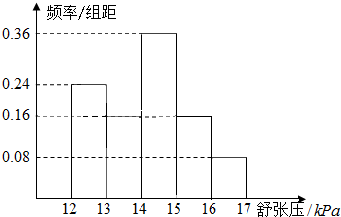
为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

| A、6 | B、8 | C、12 | D、18 |
考点:频率分布直方图
专题:概率与统计
分析:由频率=
以及直方图可得分布在区间第一组与第二组共有20人的频率,即可求出第三组中有疗效的人数得到答案;
| 频数 |
| 样本容量 |
解答:
解:由直方图可得分布在区间第一组与第二组共有20人,分布在区间第一组与第二组的频率分别为0.24,0.16,所以第一组有12人,第二组8人,第三组的频率为0.36,所以第三组的人数:18人,
第三组中没有疗效的有6人,
第三组中有疗效的有12人.
故选:C.
第三组中没有疗效的有6人,
第三组中有疗效的有12人.
故选:C.
点评:本题考查古典概型的求解和频率分布的结合,列举对事件是解决问题的关键,属中档题.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
钝角三角形ABC的面积是
,AB=1,BC=
,则AC=( )
| 1 |
| 2 |
| 2 |
| A、5 | ||
B、
| ||
| C、2 | ||
| D、1 |
已知a,b∈R,i是虚数单位,若a-i与2+bi互为共轭复数,则(a+bi)2=( )
| A、5-4i | B、5+4i |
| C、3-4i | D、3+4i |
如图所示,程序框图(算法流程图)的输出结果是( )


| A、34 | B、55 | C、78 | D、89 |
在x(1+x)6的展开式中,含x3项的系数为( )
| A、30 | B、20 | C、15 | D、10 |