题目内容

己知
e1
，
e2
是夹角为60°的两个单位向量，则
a
=2
e1
+
e2
模是（　　）
A、3
B、
5
C、
7
D、7
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积的定义和性质即可得出．
解答： 解：∵|
e1
|=|
e2
|=1，
e1
•
e2
=|
e1
| |
e2
|cos60°=1×1×
1
2
=
1
2
．
∴|
a
|=
(2
e1
+
e2
)2
=
4
e1
2+
e2
2+4
e1
•
e2
=
4×12+12+4×
1
2
=
7
．
故选：C．
点评：本题考查了数量积的定义和性质，属于基础题．
练习册系列答案
相关题目
平面内，n（n∈N*）条直线两两相交，但任意三条不交于同一点．若这n条直线将平面分成f（n）个部分，则f（3）=
 
；f（n）=
 
．
已知a＞0，函数f（x）=x3+ax2+bx+c在区间[-2，2]单调递减，则4a+b的最大值为
 
．
下列命题中，错误命题的个数有（　　）
①垂直于同一条直线的两条直线互相平行；
②平行于同一个平面的两个平面平行；
③如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面；
④如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β．
A、4B、3C、2D、1
已知直线2x+3y-3=0和4x+my+2=0互相平行，则两直线之间的距离是（　　）
A、
7
13
26
B、
5
13
26
C、
4
13
13
D、4
i为虚数单位，则(
1+i
1-i
)2015=（　　）
A、-iB、-1C、iD、1
已知集合M={x|
2
x
＞1}，N={y|y=x2+1}，则M∩N=（　　）
A、[1，2）B、（1，2）
C、（2，+∞）D、∅
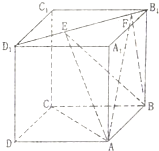如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=
2
2
，现有下列结论：
①AC⊥BE；
②平面AEF与平面ABCD的交线平行于直线EF；
③异面直线AE，BF所成的角为定值；
④三棱锥A-BEF的体积为定值，其中错误结论的个数是（　　）
A、0个B、1个C、2个D、3个
从装有n+1个球的口袋中取出m个球（0＜m≤n，m，n∈N），共有C
 
m
n+1
种取法．在这C
 
m
n+1
种取法中，可以分成一个指定的球被取到和未被取到两类：一类是该指定的球未被取到，共有C
 
0
1
•C
 
m
n
种取法；另一类是该指定的球被取到，共有C
 
1
1
•C
 
m-1
n
种取法．显然C10•Cnm+C11•Cnm-1=C
 
m
n+1
，即有等式：C
 
m
n
+C
 
m-1
n
=C
 
m
n+1
成立．试根据上述思想，则有：Cnm+Ck1•Cnm-1+Ck2•Cnm-2+…+Ckk•Cnm-k（其中当1≤k＜m≤n，k，m，n∈N）为（　　）
A、C
 
m
n+k
B、C
 
m
n+k+1
C、C
 
m+1
n+k
D、C
 
k
n+m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网