题目内容
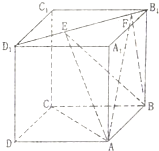如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=
| ||
| 2 |
①AC⊥BE；
②平面AEF与平面ABCD的交线平行于直线EF；
③异面直线AE，BF所成的角为定值；
④三棱锥A-BEF的体积为定值，其中错误结论的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：①AC⊥BE，可由线面垂直证两线垂直；
②由面面平行的定义可证得平面AEF与平面ABCD的交线平行于直线EF；
③异面直线AE、BF所成的角为定值，可由两个极好位置说明两异面直线所成的角不是定值．
④三棱锥A-BEF的体积为定值，可证明棱锥的高与底面积都是定值得出体积为定值；
②由面面平行的定义可证得平面AEF与平面ABCD的交线平行于直线EF；
③异面直线AE、BF所成的角为定值，可由两个极好位置说明两异面直线所成的角不是定值．
④三棱锥A-BEF的体积为定值，可证明棱锥的高与底面积都是定值得出体积为定值；
解答：
解：①AC⊥BE，由题意及图形知，AC⊥面DD1B1B，故可得出AC⊥BE，此命题正确；
②平面A1B1C1D1∥平面ABCD，设平面AEF∩平面ABCD=l，平面AEF∩A1B1C1D1=EF，故l∥EF，此命题正确；
③异面直线AE、BF所成的角为定值，由图知，当F与B1重合时，令上底面顶点为O，则此时两异面直线所成的角是∠A1AO，当E与D1重合时，此时点F与O重合，则两异面直线所成的角是OBC1，此二角不相等，故异面直线AE、BF所成的角不为定值．
④三棱锥A-BEF的体积为定值，由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD1B1B距离是定值，故可得三棱锥A-BEF的体积为定值，此命题正确；
综上知③错误，
故错误结论的个数是1个，
故选：B
②平面A1B1C1D1∥平面ABCD，设平面AEF∩平面ABCD=l，平面AEF∩A1B1C1D1=EF，故l∥EF，此命题正确；
③异面直线AE、BF所成的角为定值，由图知，当F与B1重合时，令上底面顶点为O，则此时两异面直线所成的角是∠A1AO，当E与D1重合时，此时点F与O重合，则两异面直线所成的角是OBC1，此二角不相等，故异面直线AE、BF所成的角不为定值．
④三棱锥A-BEF的体积为定值，由几何体的性质及图形知，三角形BEF的面积是定值，A点到面DD1B1B距离是定值，故可得三棱锥A-BEF的体积为定值，此命题正确；
综上知③错误，
故错误结论的个数是1个，
故选：B
点评：本题考查棱柱的结构特征，解答本题关键是正确理解正方体的几何性质，且能根据这些几何特征，对其中的点线面和位置关系作出正确判断．熟练掌握线面平行的判断方法，异面直线所成角的定义以及线面垂直的证明是解答本题的知识保证．
练习册系列答案
相关题目
己知
，
是夹角为60°的两个单位向量，则
=2
+
模是（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| A、3 | ||
B、
| ||
C、
| ||
| D、7 |
若不等式2xlnx≥-x2+ax-3对x∈（0，+∞）恒成立，则实数a的取值范围是（ ）
| A、（-∞，0） |
| B、（0，+∞） |
| C、（-∞，4] |
| D、[4，+∞） |
随机调查某校50个学生的午餐费，结果如下表，这50个学生午餐费的平均值和方差分别是（ ）
| 餐费（元） | 3 | 4 | 5 |
| 人数 | 10 | 20 | 20 |
| A、4，0.6 | ||
B、4，
| ||
| C、4.2，0.56 | ||
D、4.2，
|
已知sinx=-
，
＜x＜
，则角x=（ ）
| 1 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
方程x2+（k-2）x+5-k=0的两个不等实根都大于2，则实数k的取值范围是（ ）
| A、k＜-2 |
| B、k≤-4 |
| C、-5＜k≤-4 |
| D、-5＜k＜-4 |
cos（-1560°）的值为（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
设f（x）=x2+ax+b（a，b∈R），当x∈[-1，1]时，|f（x）|的最大值为m，则m的最小值为（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |