题目内容
1.在正方体ABCD-A1B1C1D1中,若棱长AB=3,则点B到平面ACD1的距离为$\sqrt{3}$.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出点B到平面ACD1的距离.
解答 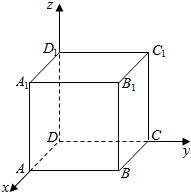 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则B(3,3,0),A(3,0,0),C(0,3,0),C1(0,3,3),D1(0,0,3),
$\overrightarrow{AC}$=(-3,3,0),$\overrightarrow{A{D}_{1}}$=(-3,0,3),$\overrightarrow{AB}$=(0,3,0),
设平面ACD1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=-3x+3y=0}\\{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=-3x+3z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,1,1),
∴点B到平面ACD1的距离:
d=$\frac{|\overrightarrow{AB}•\overrightarrow{n}|}{|\overrightarrow{AB}|•|\overrightarrow{n}|}$=$\frac{|3|}{\sqrt{3}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查点到平面的距离的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
12.甲、乙两人下棋,两人和棋的概率是$\frac{1}{2}$,乙获胜的概率是$\frac{1}{3}$,则乙不输的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
9.“?x∈R,x2-2>0”的否定是( )
| A. | ?x∈R,x2-2<0 | B. | ?x∈R,x2-2≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{2}$-2<0 | D. | ?x0∈R,x${\;}_{0}^{2}$-2≤0 |
13.400辆汽车通过某公路时,时速的频率分布直方图如图所示,则时速在[60,80)的汽车大约有( )
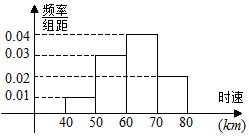

| A. | 120辆 | B. | 140辆 | C. | 160辆 | D. | 240辆 |
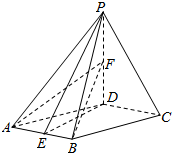 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.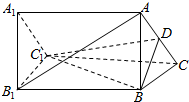 已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.
已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.