题目内容
2.已知关于x的不等式ax-b<0的解集是(3,+∞),则关于x的不等式$\frac{ax+b}{x-2}≥0$的解集是[-3,2).分析 由题意可得a<0,且 $\frac{b}{a}$=3,关于x的不等式$\frac{ax+b}{x-2}≥0$,转化为$\frac{x+3}{x-2}$≤0,解得即可.
解答 解:∵关于x的不等式ax-b<0,即 ax<b的解集是(3,+∞),
∴a<0,且 $\frac{b}{a}$=3.
∴关于x的不等式$\frac{ax+b}{x-2}≥0$,即$\frac{x+\frac{b}{a}}{x-2}$≤0,即$\frac{x+3}{x-2}$≤0,即 (x+3)(x-2)≤0,且x-2≠0,
求得-3≤x<2,
故答案为:[-3,2).
点评 本题主要考查分式不等式的解法,体现了等价转化的数学思想,属于基础题.

练习册系列答案
相关题目
12.甲、乙两人下棋,两人和棋的概率是$\frac{1}{2}$,乙获胜的概率是$\frac{1}{3}$,则乙不输的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
13.400辆汽车通过某公路时,时速的频率分布直方图如图所示,则时速在[60,80)的汽车大约有( )
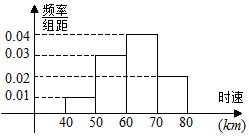

| A. | 120辆 | B. | 140辆 | C. | 160辆 | D. | 240辆 |
17. 甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
 甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )| A. | $\overline{x_1}$>$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ | B. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$>$S_2^2$ | ||
| C. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$=$S_2^2$ | D. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ |
12.下列关于语句的说法正确的是( )
| A. | 在程序中,程序执行的顺序是按照程序中语句行排列的顺序执行的 | |
| B. | 条件语句就是满足条件就执行,不满足条件就不执行 | |
| C. | 循环语句是流程图中循环结构的实现 | |
| D. | 循环结构不可以嵌套 |
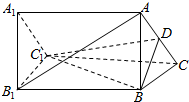 已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.
已知如图,ABC-A1B1C1是正三棱柱,D是AC的中点.