题目内容
4.已知集合M={x||x|≤2},N={x|x2+2x-3≤0},则M∩N=( )| A. | {x|-2≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1≤x≤2} | D. | {x|-3≤x≤2} |
分析 先分别求出集合M,N,由此利用交集定义能求出M∩N.
解答 解:∵集合M={x||x|≤2}={x|-2≤x≤2},
N={x|x2+2x-3≤0}={x|-3≤x≤1},
∴M∩N={x|-2≤x≤1}.
故选:A.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在△ABC的三边分别为a,b,c,a2=b2+c2-bc,则A等于( )
| A. | 30° | B. | 60° | C. | 75° | D. | 120° |
12.已知直线a,b和平面α,则下列命题正确的是( )
| A. | 若a∥b,b∥α,则a∥α | B. | a⊥b,b⊥α,则a∥α | C. | 若a∥b,b⊥α,则a⊥α | D. | 若a⊥b,b∥α,则a⊥α |
9.设实数x,y满足$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{y≥x}\end{array}\right.$,则x+2y的最小值为( )
| A. | 1.5 | B. | 2 | C. | 5 | D. | 6 |
14.已知直线l1:(a+2)x+3y=5与直线l2:(a-1)x+2y=6平行,则a等于( )
| A. | -1 | B. | 7 | C. | $\frac{7}{5}$ | D. | 2 |
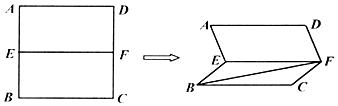 如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.
如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.